Voor \(f(x,y)=x^3+7x^2y+3xy^5-5y^6\) zijn de partiële afgeleiden:
\begin{gather*}
\frac{\partial f(x,y)}{\partial x } = 3x^2+14xy+3y^5\\
\frac{\partial f(x,y)}{\partial y } = 7x^2+15xy^4-30y^5
\end{gather*}
Sectie 4.5 Impliciet afleiden en raaklijnen aan krommen
Gegeven de ellips met vergelijking
\begin{equation*}
\frac{x^2}{9}+\frac{y^2}{4}=1
\end{equation*}
Deze ellips is niet de grafiek van een functie, maar bovenstaande vergelijking definieert impliciet wel twee verschillende functies. Stel dat we de vergelijking van de raaklijn in een punt van de ellips willen berekenen, dan kunnen we deze functievoorschriften expliciet bepalen en vervolgens de afgeleiden berekenen.
\begin{equation*}
\frac{x^2}{9}+\frac{y^2}{4}=1 \Rightarrow \begin{cases} f_1(x) = \frac{2}{3} \sqrt{9-x^2} \\ f_1(x) = - \frac{2}{3} \sqrt{9-x^2} \end{cases}
\end{equation*}
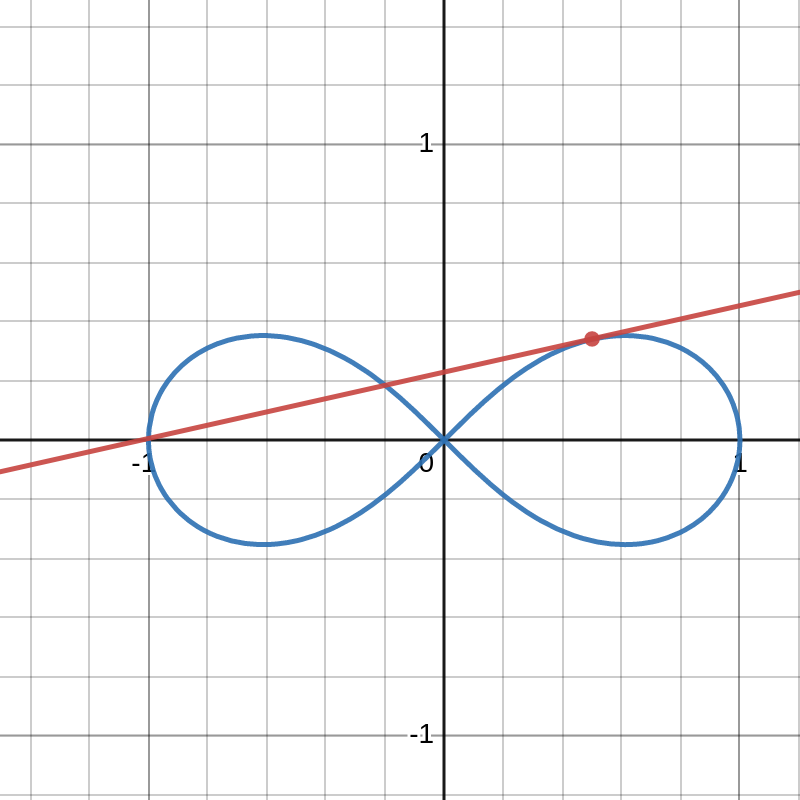
De grafiek van \(f_1\) is de bovenkant van de ellips en de grafiek van \(f_2\) de onderkant. Deze functies zijn vrij gemakkelijk te bepalen en af te leiden, maar voor bijvoorbeeld de lemniscaat met vergelijking
1
Dit komt later nog aan bod.
\begin{equation*}
\left(x^{2}+y^{2}\right)^{2}= x^{2}-y^{2}
\end{equation*}
is deze manier van werken een pak minder evident. We bekijken dus even een algemenere manier om raaklijnen in punten van krommen te bepalen.
We werken het voorbeeld van de ellips met vergelijking \(\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\) verder uit. Het linkerlid van deze vergelijking kan beschouwd worden als het functievoorschrift van een functie \(f\) in twee veranderlijken:
\begin{equation*}
f: \mathbb{R}^2 \to \mathbb{R}: (x,y) \to z=f(x,y)
\end{equation*}
We noemen de partiële afgeleide van \(f\) naar \(x\text{,}\) de afgeleide van \(f(x,y)\) naar \(x\) waarbij de variabele \(y\) als constant beschouwd wordt. We noteren dit als volgt
\begin{equation*}
\frac{\partial z }{\partial x}=\frac{\partial f(x,y)}{\partial x}
\end{equation*}
Analoog is de partiële afgeleide van \(f\) naar \(y\text{,}\) de afgeleide van \(f(x,y)\) naar \(y\text{,}\) waarbij \(x\) als constant verondersteld wordt:
\begin{equation*}
\frac{\partial z }{\partial y}=\frac{\partial f(x,y)}{\partial y}
\end{equation*}
Voor \(f(x,y)=\dfrac{x^2}{9}+\dfrac{y^2}{4}\) geeft dit
\begin{gather*}
\frac{\partial z }{\partial x} = \frac{2x}{9}\\
\frac{\partial z }{\partial y} = \frac{y}{2}
\end{gather*}
Voorbeeld 4.5.1. Partiële afgeleiden.
De grafiek van een functie \(z=f(x,y)\) stelt een oppervlak in de ruimte voor en de partiële afgeleide naar \(x(y)\) in een bepaald punt \((x_1,y_1)\) is dan de richtingscoëfficiënt van de raaklijn volgens de \(x(y)\)-as aan het oppervak in dit punt. Volg deze link voor een visualisatie in Geogebra. De infinitesimale verandering van de functiewaarde \(z\) in functie van de infinitesimale veranderingen \(dx\) en \(dy\) noemen we de totale differentiaal en wordt als volgt berekend:
2
www.geogebra.org/3d/q5qg8ajw
\begin{equation*}
dz=df(x,y)=\frac{\partial f }{\partial x} \; dx +\frac{\partial f}{\partial y} \; dy
\end{equation*}
Voor alle punten op de gegeven ellips geldt er echter dat \(z=1\) en de totale differentiaal is dus gelijk aan nul. Uit \(dz=0\) volgt dan het verband tussen \(dy\) en \(dx\) en bijgevolg een uitdrukking voor de afgeleide \(\frac{dy}{dx}\text{:}\)
\begin{align*}
\amp \frac{\partial f }{\partial x} \; dx +\frac{\partial f}{\partial y} \; dy = 0 \\
\Rightarrow \amp \frac{2x}{9} \; dx +\frac{y}{2} \; dy = 0 \\
\Leftrightarrow \amp \frac{dy}{dx} = - \frac{-4x}{9y}
\end{align*}
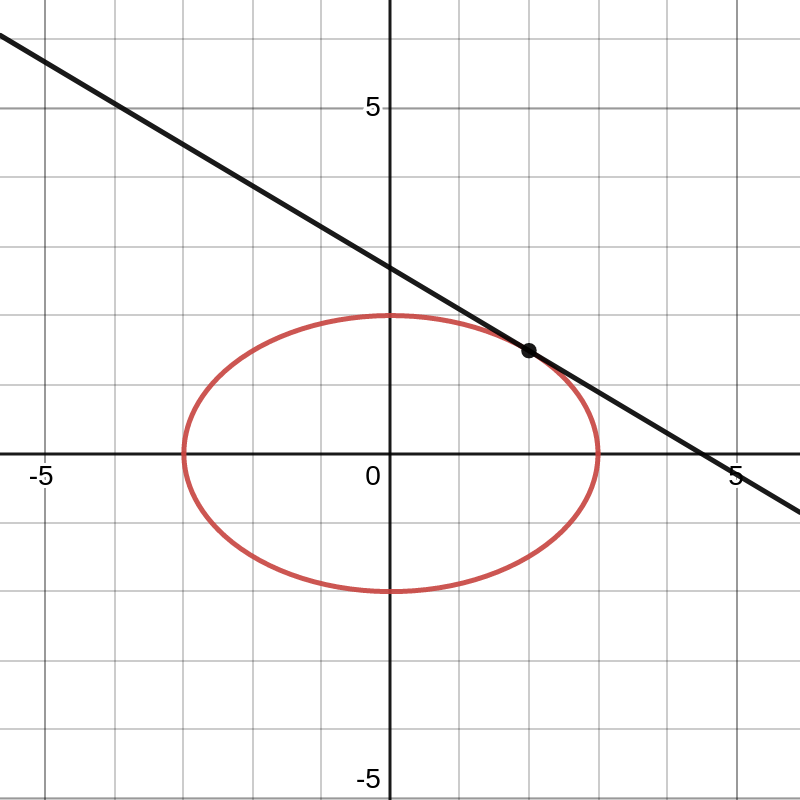
Beschouwen we nu het punt \(\left(2,\frac{2\sqrt{5}}{3}\right)\text{,}\) dan is de vergelijking van de raaklijn aan de ellips in dit punt gelijk aan
\begin{equation*}
y=\frac{-8}{6\sqrt{5}}(x-2)+\frac{2\sqrt{5}}{3}=-\frac{4}{3\sqrt{5}}x+\frac{6}{\sqrt{5}}
\end{equation*}
Impliciet afleiden.
Gegegeven een kromme met cartesische vergelijking \(f(x,y)=0\text{.}\) De afgeleide \(\dfrac{dy}{dx}\) kan je bepalen door de uitdrukking
\begin{equation*}
\frac{\partial f }{\partial x} \; dx +\frac{\partial f}{\partial y} \; dy = 0
\end{equation*}
om te vormen.
