Met behulp van deze twee rekenregels kunnen we snel de afgeleide van een veeltermfunctie berekenen:
\begin{equation*}
D(2x^3-4x^2+5x)=2D(x^3)-4D(x^2)+5D(x)=6x^2-8x+5
\end{equation*}
Sectie 4.2 Rekenregels voor het afleiden van functies
Het berekenen van de afgeleide van een functie via de definitie neemt in de meeste gevallen heel wat tijd in beslag. We zullen daarom een aantal rekenregels afleiden die het rekenwerk eenvoudiger maken.
In de vorige paragraaf hebben we aangetoond dat
1
zie oefeningen
\begin{align*}
\amp D(x) = 1 \\
\amp D(x^2) = 2x \\
\amp D(x^3) = 3x^2 \\
\amp D\left(x^{-1} \right) = -x^{-2} \\
\amp D\left(x^{-2} \right) = -2x^{-3}
\end{align*}
We nemen voorlopig zonder bewijs aan dat
\begin{equation*}
\displaystyle \boxed{D(x^n)=nx^{n-1} \quad (n \in \mathbb{Z}_0)}
\end{equation*}
Er geldt bovendien ook dat
\begin{equation*}
\boxed{D(c)=0 \quad \text{voor alle} \quad c \in \mathbb{R}}
\end{equation*}
De eerste twee rekenregels zijn intuïtief eenvoudig te begrijpen:
\begin{align*}
\amp \boxed{ D(c \cdot f)=c \cdot Df \quad (c \in \mathbb{R})}\\
\amp \boxed{ D(f+g)=Df+Dg}
\end{align*}
Voorbeeld 4.2.1.
Opdracht 4.2.1.
(7u) Bewijs bovenstaande rekenregels.
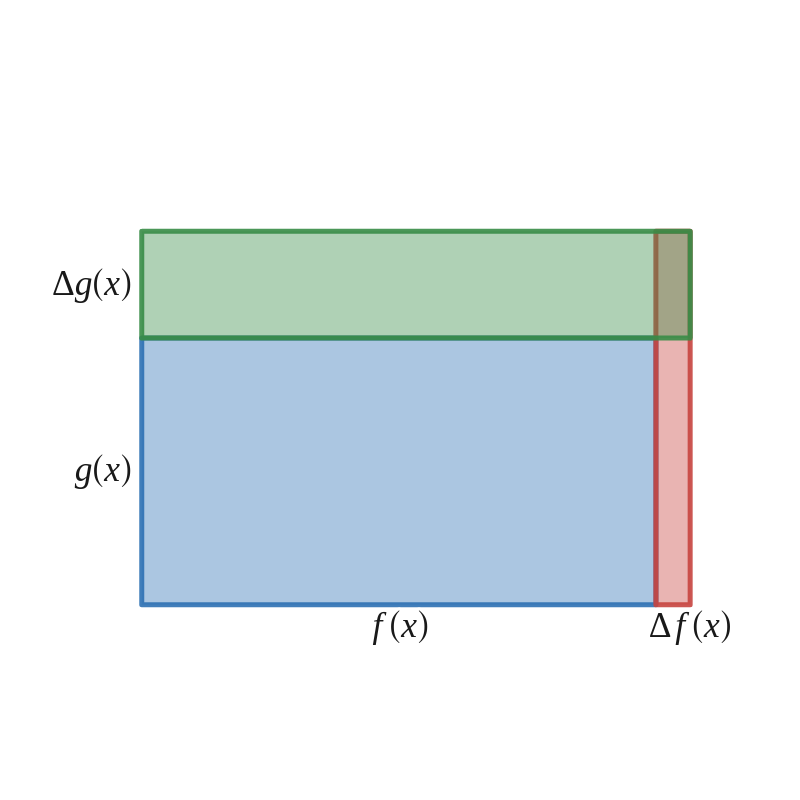
De formule voor de afgeleide van een product is op het eerste zicht minder intuïtief en vergt wat extra denkwerk. We stellen \(h(x)=f(x) \cdot g(x)\) en interpreteren \(h(x)\) als de oppervlakte van een rechthoek met lengte \(f(x)\) en breedte \(g(x)\text{.}\) Als het argument \(x\) toeneemt met \(\Delta x\text{,}\) dan veranderen ook de afmetingen van de rechthoek met \(\Delta f(x)\) en \(\Delta g(x)\) (we tekenen de verandering hier positief). De verandering van de functiewaarde is dan gelijk aan de verandering van de oppervlakte van de rechthoek:
\begin{equation*}
\Delta y = \Delta h(x) = \Delta f(x) \cdot g(x) + f(x) \cdot \Delta g(x) + \Delta f(x) \cdot \Delta g(x)
\end{equation*}
We delen door \(\Delta x\text{:}\)
\begin{equation*}
\frac{\Delta h(x)}{\Delta x} = \frac{\Delta f(x)}{\Delta x} g(x) + f(x) \frac{\Delta g(x)}{\Delta x}+ \frac{\Delta f(x)}{\Delta x} \Delta g(x)
\end{equation*}
en nemen de limiet \(\Delta x \to 0\text{:}\)
\begin{align*}
\amp \lim_{\Delta x \to 0} \frac{\Delta h(x)}{\Delta x} = Dh(x)\\
\amp \lim_{\Delta x \to 0} \frac{\Delta f(x)}{\Delta x} = Df(x)\\
\amp \lim_{\Delta x \to 0} \frac{\Delta g(x)}{\Delta x} = Dg(x)\\
\amp \lim_{\Delta x \to 0} \Delta g(x) = 0
\end{align*}
Hieruit volgt de productregel voor het afleiden van funties
\begin{equation*}
\boxed{ D(f \cdot g)=Df \cdot g + f \cdot Dg }
\end{equation*}
Opdracht 4.2.2.
(7u) Bewijs de productregel zonder het product meetkundig te interpreteren. Tip: voeg volgende termen toe aan \(\Delta h\text{:}\) \(-f(x)g(x+\Delta x) + f(x) g(x+\Delta x)\text{.}\)
Opdracht 4.2.3.
Bereken de afgeleide functie van
(a)
\(\displaystyle f(x)=-3x^5\)
(b)
\(\displaystyle f(x)=6x^4-2x^3+x+1\)
(c)
\(\displaystyle f(x)=(5x^3-4x^2-x)(-2x+1)\)
(d)
\(\displaystyle f(x)=3(x^2+1)(2x^2-1)(2x+3)\)
Opdracht 4.2.4.
Gebruik de productregel om aan te tonen dat \(D(c \cdot f) =c \cdot Df\)
Stel dat je de functie \(f(x)=(2x^4+3)^5\) wil afleiden. Je zou natuurlijk de vijfde macht kunnen uitrekenen, maar het resultaat is een veeltermfunctie van de twintigste graad, dus dat geeft een hoop rekenwerk. We gaan dus op zoek naar een efficiëntere manier om samengestelde functies af te leiden. Het basisidee is eenvoudig: stel \(u=2x^4+3\) en bereken \(\dfrac{dy}{dx}\) in twee stappen als volgt: \(\dfrac{dy}{du} \cdot \dfrac{du}{dx} \text{.}\) De verandering van \(y\) i.f.v. \(x\) is gelijk aan de verandering van \(y\) i.f.v \(u\) maal de verandering van \(u\) i.f.v. \(x\text{.}\)
\begin{align*}
\amp \; u = 2x^4 + 3 \Rightarrow \frac{du}{dx} = 8x^3\\
\amp \; y=u^5 \Rightarrow \frac{dy}{du} = 5 u^4\\
\Rightarrow \amp \; \frac{dy}{dx} = 5u^4 \cdot 8x^3 = 5(2x^4+3)^4 \cdot 8x^3
\end{align*}
Merk op dat we hier voor de duidelijkheid expliciet de variabele waarnaar we afleiden noteren.
Stel dat je algemeen een samengestelde functie \((g \circ f)\) wil afleiden, dan stel je \(u=f(x)\text{.}\) Als het argument \(x\) verandert met \(\Delta x\text{,}\) dan is \(\Delta u\) de verandering van de functiewaarde van \(f\) en kan je schrijven dat
\begin{align*}
D[g(f(x))] = \amp \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} \\
= \amp \left ( \lim_{\Delta u \to 0} \frac{\Delta y}{\Delta u} \right ) \cdot \left ( \lim_{\Delta x \to 0} \frac{\Delta u}{\Delta x} \right ) \\
= \amp Dg(u) \cdot Df(x)\\
= \amp Dg(f(x)) \cdot Df(x)
\end{align*}
Dit noemen we de kettingregel:
\begin{equation*}
\boxed{D[g(f(x))] = Dg(f(x)) \cdot Df(x)} \qquad \text{of} \qquad \boxed{\frac{dy}{dx}= \frac{dy}{du} \cdot \frac{du}{dx}}
\end{equation*}
Om de kettingregel toe te passen, kan je de substitutie expliciet volledig uitschrijven zoals hierboven of je baseren op de uitgeschreven samenstelling zoals hieronder:
Voorbeeld 4.2.2. Kettingregel.
Als tweede voorbeeld leiden we de functie \(f(x)=((2x-1)^4+3)^5\) af. Nu moeten we de kettingregel twee keer toepassen:
\begin{align*}
\amp y = u^5 \Rightarrow \frac{dy}{du} = 5u^4\\
\amp u = (2x-1)^4 +3 = v^4 +3 \Rightarrow \frac{du}{dv}=4v^3\\
\amp v = 2x-1 \Rightarrow \frac{dv}{dx}=2\\
\Rightarrow \; \amp \frac{dy}{dx} = 5((2x-1)^4+3)^4 \cdot 4(2x-1)^3 \cdot 2
\end{align*}
Voorbeeld 4.2.3. Rekenregels combineren.
We bekijken nu een complexer voorbeeld waar je verschillende rekenregels moet combineren: het berekenen van de afgeleide van de functie \(\displaystyle f(x)=\frac{(x^4-2x)^3}{5x-1}\text{.}\) \(f\) is het product van twee functies \(g_1\) en \(g_2\) met \(g_1\) en \(g_2\) twee samengestelde functies. Je past dus eerst de productregel toe en vervolgens twee keer de kettingregel:
\begin{align*}
\amp Df(x) = Dg_1(x) \cdot g_2(x) + g_1(x) \cdot Dg_2(x) \\
\amp g_1(x) = (x^4-2x)^3 \Rightarrow Dg_1(x) = 3(x^4-2)^2 \cdot (4x^3 -2) \\
\amp g_2(x) = (5x-1)^{-1} \Rightarrow Dg_2(x) = -(5x-1)^{-2} \cdot 5 \\
\Rightarrow \; \amp Df(x) = 3(x^4-2)^2 \cdot (4x^3 -2) \cdot (5x-1)^{-1} - (x^4-2x)^3 \cdot (5x-1)^{-2} \cdot 5
\end{align*}
