Sectie 5.2 De cosinusfunctie
De grafiek van de cosinusfunctie ontstaat door de koppels \(\left(x,\cos\left(x\right)\right)\) uit te zetten met \(x\) de lengte van de cirkelboog van \((1,0)\) tot \((\cos x,\sin x)\text{.}\)
Merk op dat \(\cos x=\sin \left(x+\dfrac{\pi}{2}\right)\text{.}\) De cosinusfunctie is dus eigenlijk gewoon een verschoven sinusfunctie.
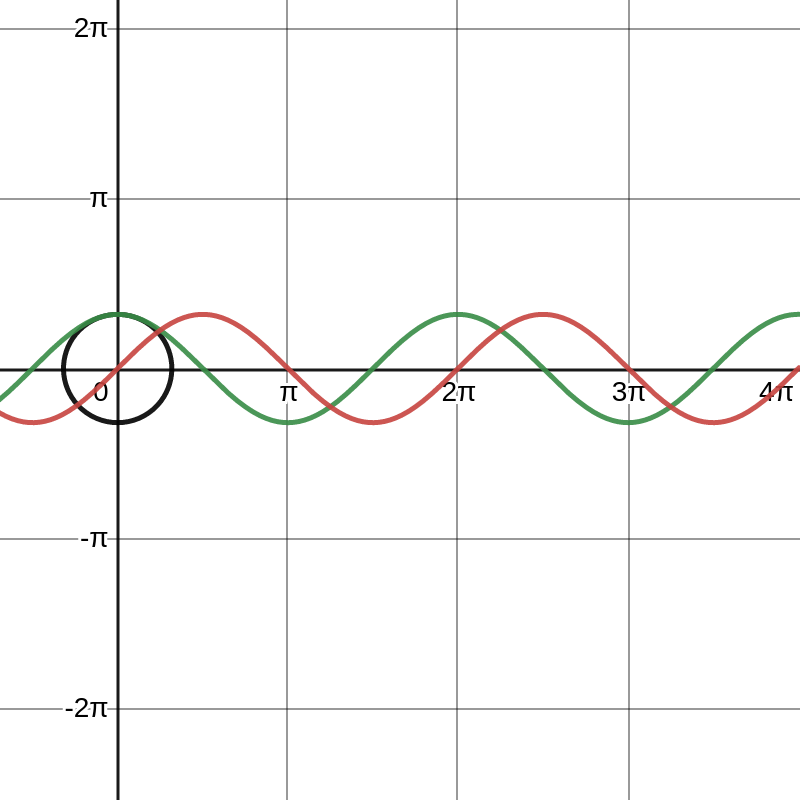
Het domein van de cosinusfunctie is \(\mathbb{R}\text{,}\) het bereik is het interval \([-1,1]\text{,}\) de nulwaarden zijn \(\dfrac{\pi}{2} + k \pi\) met \(k \in \mathbb{Z}\text{,}\) de lokale maxima worden bereikt in \(2k\pi\) met \(k \in \mathbb{Z}\) en de lokale minima in \(\pi+2k\pi\) met \(k \in \mathbb{Z}\text{.}\)
