Sectie 3.2 Structuur van veeltermfuncties
Lineaire en onontbindbare kwadratische functies zijn de bouwstenen van de veeltermfuncties. Dit betekent dat elke veeltermfunctie \(f(x)=a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0\) als volgt kan geschreven worden als een product van lineaire functies en onontbindbare kwadratische functies:
\begin{equation*}
\boxed{f(x)= a_n(x-x_1)(x-x_2) \ldots ((x-p_1)^2+q_1)((x-p_2)^2+q_2)\ldots}
\end{equation*}
\(x_i\) zijn de nulwaarden van \(f\) en alle \(q_i\) zijn groter dan nul aangezien de kwadratische functies onontbindbaar zijn. De grafieken van de functies \(g_i(x)=x-x_i\) zijn rechten door \((x_i,0)\) en met richtingscoëfficiënt 1; de grafieken van de functies \(h_i(x)=(x-p_i)^2+q_1\) zijn dalparabolen met top \((p_i,q_i)\text{.}\) De coëfficiënt \(a_n\) bepaalt de herschaling volgens de \(y\)-richting.
We bespreken eerst de derdegraads veeltermfuncties. Het functievoorschrift bevat dan maximaal drie lineaire factoren.
-
De functie \(f(x)=15x^3-44x^2-5x+6\) kan geschreven worden als \(f(x)=15(x-3) \left (x+\dfrac{2}{5} \right) \left (x-\dfrac{1}{3} \right )\text{.}\) De nulwaarden van \(f\) zijn dus \(3\text{,}\) \(-\dfrac{2}{5}\) en \(\dfrac{1}{3}\) en de corresponderende nulpunten \((3,0)\text{,}\) \(\left (-\dfrac{2}{5},0 \right )\) en \(\left ( \dfrac{1}{3},0 \right)\text{.}\) De grafiek van \(f\) snijdt de \(x\)-as in elk nulpunt en de tekentabel van \(f\) ziet er als volgt uit:
Het teken rechts van de grootste nulwaarde wordt bepaald door het teken van de coëfficiënt \(a_n\text{.}\) Voor dit voorbeeld is \(a_3=15\) en we starten dus met een positief teken.
-
Als een lineaire factor twee keer voorkomt zoals bijvoorbeeld bij de functie \(f(x)=15(x-3)^2 \left (x+\dfrac{2}{5} \right )\text{,}\) dan noemen we \(3\) een nulwaarde met multipliciteit 2 (of een tweevoudige nulwaarde). De grafiek van \(f\) raakt nu in \((3,0)\) aan de \(x\)-as en we noemen dit nulpunt dan ook een raakpunt van de grafiek aan de \(x\)-as. De tekentabel van \(f\) heeft nu maar één tekenwissel:
-
Als een lineaire factor drie maal voorkomt, zoals bijvoorbeeld bij de functie \(f(x)=15(x-3)^3\text{,}\) dan noemen we \(3\) een nulwaarde met multipliciteit 3 (of een drievoudige nulwaarde). De grafiek van \(f\) raakt in dit geval niet alleen aan de \(x\)-as in het punt \((3,0)\text{,}\) maar buigt er als het ware ook doorheen. Een dergelijk nulpunt wordt een buigpunt genoemd . De tekentabel toont nu de drievoudige nulwaarde en één tekenwissel:
-
Een derdegraadsfunctie kan nooit exact twee lineaire factoren hebben en geen enkele lineaire factor is eveneens onmogelijk. De enige mogelijkheid die dan nog overblijft is een lineaire factor en een onontbindbare kwadratische factor, zoals bijvoorbeeld bij de functie \(f(x)=(x-3)((x+1)^2+2)\text{.}\)
Het bespreken van veeltermfuncties met een graad hoger dan drie verloopt volledig analoog. We zetten kort de belangrijkste kenmerken van vierdegraadsveeltermfuncties op een rijtje.
-
Veronderstel dat je een veeltermfunctie \(f\) van de vierde graad kan ontbinden in vier lineaire factoren. Elke enkelvoudige nulwaarde correspondeert dan met een snijpunt van de grafiek van \(f\) met de \(x\)-as, elke tweevoudige nulwaarde met een raakpunt en elke drievoudige nulwaarde met een buigpunt. Beschouw bijvoorbeeld de functie \(f(x)=(x+1)^2(x-3)^2\) (twee raakpunten) en de functie \(f(x)=(x+1)(x-3)^3\) (één snijpunt en één buigpunt):
-
Een viervoudige nulwaarde is nu ook mogelijk en correspondeert opnieuw met een raakpunt. Ter illustratie hiernaast de grafiek van de functie \(f(x)=(x-3)^4\text{.}\) Merk op dat deze grafiek (in volle lijn) wel veel sneller stijgt dan de grafiek van \(f(x)=(x-3)^2\) (in streepjeslijn).
-
Eén onontbindbare kwadratische factor kan voorkomen in combinatie met twee verschillende of twee gelijke lineaire factoren. Dit wordt hieronder geïllustreerd voor de functies \(f(x)=(x^2+2)(x+3)(x-3)\) en \(f(x)=(x^2+2)(x-3)^2\text{.}\)
-
Tenslotte kan een veeltermfunctie van de vierde graad ook bestaan uit het product van twee onontbindbare kwadratische factoren. Bijvoorbeeld \(f(x)=-2(x^2+2)((x-3)^2+1)\text{.}\)
Algemeen kunnen we de volgende besluiten trekken over de structuur van veeltermfuncties:
Eigenschappen van veeltermfuncties.
Een veeltermfunctie van oneven graad heeft minstens één nulwaarde.
De grafiek van een veeltermfunctie snijdt de \(x\)-as in het nulpunt \((x_1,0)\) als \(x_1\) een enkelvoudige nulwaarde van \(f\) is. Dit betekent dat de ontbinding van \(f(x)\) een factor \((x-x_1)\) bevat.
De grafiek van een veeltermfunctie heeft een raakpunt \((x_1,0)\) aan de \(x\)-as als \(x_1\) een nulwaarde met een even multipliciteit is. Dit betekent dat de ontbinding van \(f(x)\) een factor \((x-x_1)^k\) bevat met \(k=2,4,6, \ldots\text{.}\)
De grafiek van een veeltermfunctie heeft een buigpunt \((x_1,0)\) aan de \(x\)-as als \(x_1\) een nulwaarde met een oneven multipliciteit groter dan één is. Dit betekent dat de ontbinding van \(f(x)\) een factor \((x-x_1)^k\) bevat met \(k=3,5,7, \ldots\text{.}\)
Het teken rechts van de grootste nulwaarde in de tekentabel is gelijk aan het teken van \(a_n\text{.}\)
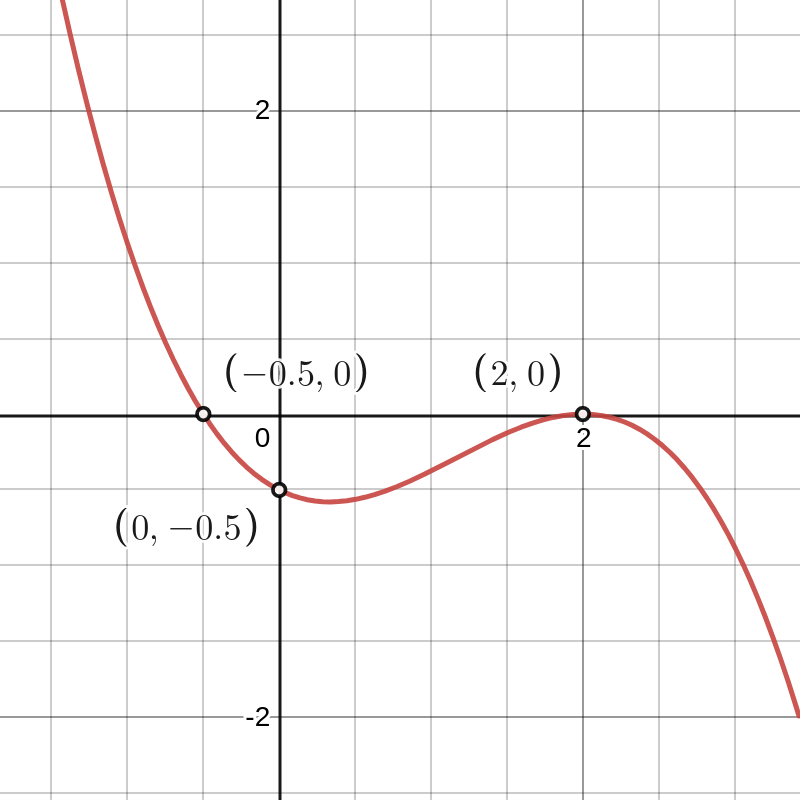
Voorbeeld 3.2.1. Functievoorschrift van een veeltermfunctie bepalen.
De figuur hiernaast toont de grafiek van een veeltermfunctie van de derde graad. De grafiek snijdt de \(x\)-as in het punt \(\left (-\dfrac{1}{2},0 \right)\) en raakt de \(x\)-as in het punt \((2,0)\text{.}\) Dit betekent dat het functievoorschrift de volgende vorm heeft:
\begin{equation*}
f(x)=a \left (x+\dfrac{1}{2} \right ) (x-2)^2
\end{equation*}
Invullen van het punt \((0,-\dfrac{1}{2})\) geeft
\begin{equation*}
-\dfrac{1}{2} =a \dfrac{1}{2} \cdot 4 \Leftrightarrow a=-\dfrac{1}{4}
\end{equation*}