Sectie 2.7 Stuksgewijs gedefinieerde functies
Een stuksgewijs gedefinieerde functie is een functie met een meervoudig functievoorschrift. De absolute waarde functie is hiervan een een eenvoudig voorbeeld. Er geldt immers dat
\begin{equation*}
f(x)=|x|=\begin{cases} x \qquad \text{als } x \ge 0 \\ -x \qquad \text{als } x \lt 0 \end{cases}
\end{equation*}
Hieronder zie je hoe je de functie
\begin{equation*}
f(x) = \begin{cases} 2x+3 \qquad \text{als } -4 \le x \le -1 \\ x^2 \qquad \text{als } -1 \lt x \le 2 \end{cases}
\end{equation*}
kan definiëren in Desmos.
Als je op een weekdag voor 19:00 in de rode zone van een stad wil parkeren betaal je 2,50 euro voor één uur; 6,00 euro voor 2 uur en 10,00 euro voor 3 uur. In \(x=1\) en \(2\) vertoont de grafiek van de functie die de kostprijs voorstelt een sprong. We zeggen dat de functie discontinu is in deze punten.
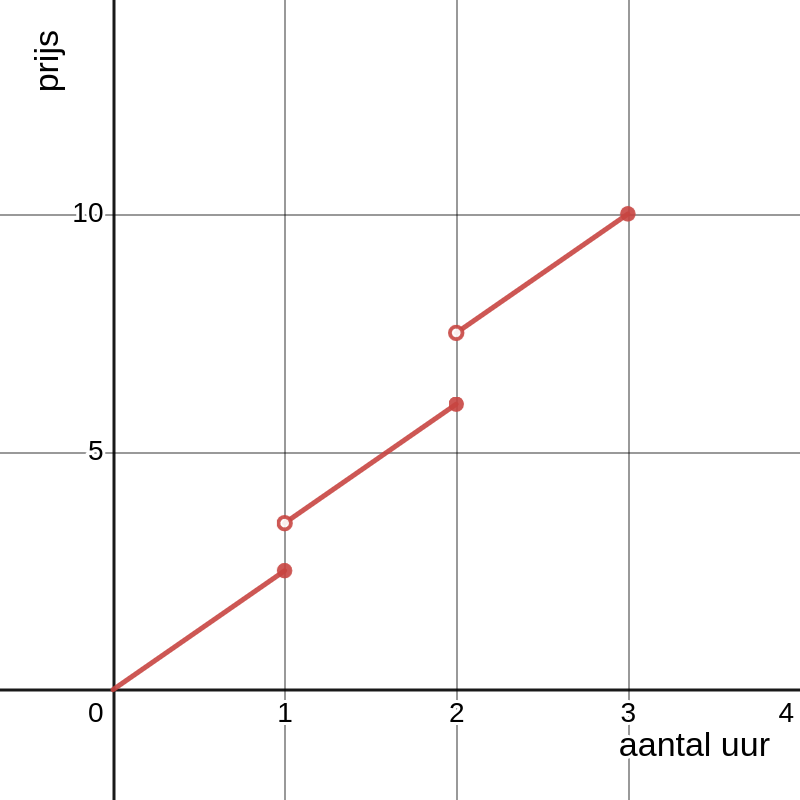
Een functie \(f\) is continu in een punt \(x=c\) van zijn domein als je de grafiek door \((c,f(c))\) kan tekenen zonder je potlood op te heffen. Als dat niet het geval is, dan zeggen we dat \(f\) discontinu is in \(c\text{.}\) Merk op dat we niet zeggen dat de functie \(f(x)=\dfrac{3}{x+2}\) discontinu is in \(x=-2\) omdat \(-2\) niet behoort tot het domein van \(f\text{.}\) We zeggen dus dat deze functie continu is in elk punt van zijn domein.
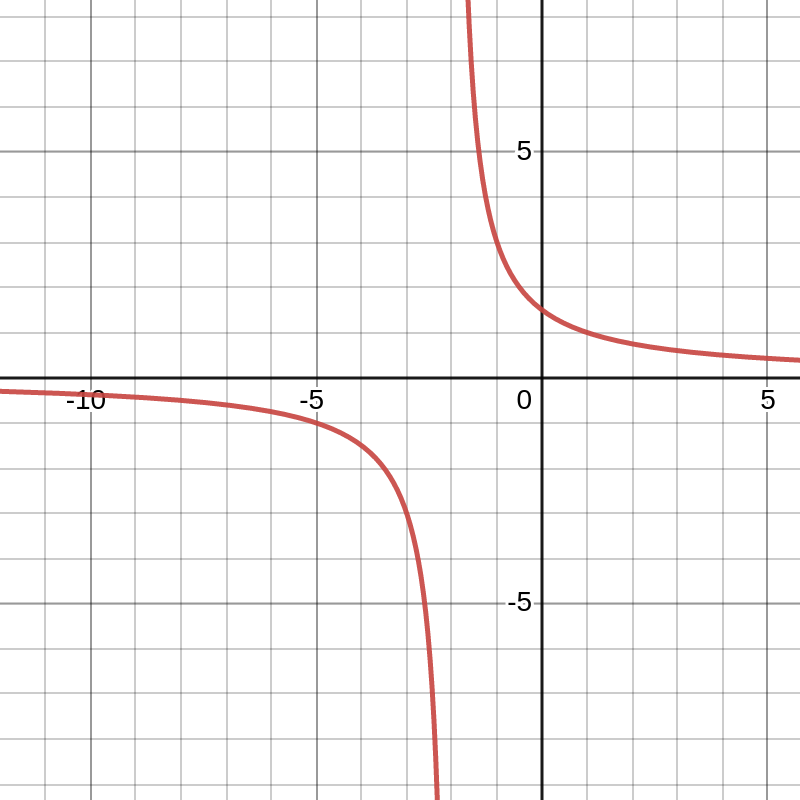
Eigenlijk zijn alle elementaire functies die je zal tegenkomen continu in alle punten van hun domein. Discontinuïteiten zullen we enkel tegenkomen bij stuksgewijs gedefinieerde functies.
