Naar de hoofdinhoud

Analyse: 3de graad ASO met 5 of 7 lesuren per week

Nele Vermeulen

Sectie 3.1 Kwadratische functies en parabolen

Vorig jaar heb je vrij uitgebreid kwadratische functies bestudeerd. We herhalen deze leerstof even kort met het oog op de uitbreiding naar veeltermfuncties. Als je deze herhaling wat te beknopt vindt, kan je deze link
 1 
wiskundeacademie.nl/onderwerpen/kwadraatafsplitsen
en ook deze link
 2 
wiskundeacademie.nl/onderwerpen/kwadratische-vergelijkingen
volgen voor gedetailleerdere uitlegfilmpjes.

Subsectie 3.1.1 Van standaardvorm naar topvorm

Een kwadratische functie \(f\) met standaard functievoorschrift \(f(x)=ax^2+bx+c\) (\(a \neq 0\)) kan altijd geschreven worden als
\begin{equation*} f(x)=a(x-p)^2+q \end{equation*}
In deze vorm is \(f\) expliciet geschreven als een samenstelling:
\begin{equation*} f = f_4 \circ f_3 \circ f_2 \circ f_1 \end{equation*}
met
\begin{align*} \amp f_1(x)=x-p\\ \amp f_2(x)=x^2\\ \amp f_3(x)=ax\\ \amp f_4(x)=x+q \end{align*}
De parabool \(y=x^2\) wordt dus getransformeerd in de grafiek van \(f\) door
  • een spiegeling om de \(x\)-as als \(a \lt 0\text{;}\)
  • een herschaling met een factor \(|a|\) volgens de \(y\)-as;
  • een verschuiving volgens de \(x\)-as met \(p\) eenheden naar rechts als \(p \gt 0\) of naar links als \(p \lt 0\text{;}\)
  • en een verschuiving volgens de \(y\)-as met \(q\) eenheden naar boven als \(q \gt 0\) of naar beneden als \(q \lt 0\text{.}\)
Hieruit volgt onmiddelijk dat \((p,q)\) de top van de parabool is en \(x=p\) de symmetrie-as.

Topvorm van een kwadratische functie.

De topvorm van een kwadratische functie is
\begin{equation*} f(x)=a(x-p)^2+q \qquad (a \neq 0) \end{equation*}
met
  • \((p,q)\) de coördinaat van de top;
  • \(x=p\) de symmetrie-as;
De grafiek van \(f\) is een
  • dalparabool als \(a \gt 0\) en een
  • bergparabool als \(a \lt 0\)
Een kwadratische functie in de topvorm \(f(x)=a(x-p)^2+q\) schrijven verloopt vrij analoog aan het oplossen van \(ax^2+bx+c=0\) door het kwadraat te vervolledigen. We illustreren dit eerst met twee voorbeelden vooraleer we het algemene geval aanpakken.

Voorbeeld 3.1.1. Een kwadratische functie in de topvorm schrijven.

Beschouw bijvoorbeeld de functie \(f(x)=x^2+2x+2\text{.}\) Aangezien \((x+1)^2=x^2+2x+1\text{,}\) kunnen we schrijven dat
\begin{equation*} x^2+2x+2=(x+1)^2+1 \end{equation*}
waarbij we de identiteit \(\boxed{(a \pm b)^2=a^2 \pm 2ab+b^2}\) gebruikt hebben.
Een iets moeilijker voorbeeld:
\begin{align*} -2x^2-4x+16 = \; \amp-2 (x^2+2x) + 16 \\ = \; \amp-2 \left [ (x+1)^2 -1 \right ] + 16 \\ = \; \amp-2 (x+1)^2 + 18 \end{align*}
We passen bovenstaande manier van werken nu toe op een algemene kwadratische functie:
\begin{align*} f(x) = \; \amp ax^2+bx+c\\ = \; \amp a \left (x^2+\dfrac{b}{a}x \right )+c \\ = \; \amp a\left [ \left (x+\dfrac{b}{2a} \right )^2 - \dfrac{b^2}{4a^2}\right ]+c \\ = \; \amp a \left (x+\dfrac{b}{2a} \right )^2 - \dfrac{b^2}{4a} +\dfrac{4ac}{4a}\\ = \; \amp a \left (x+\dfrac{b}{2a} \right )^2 - \dfrac{D}{4a} \end{align*}
In de laatste stap hebben we de discriminant \(\boxed{D=b^2-4ac}\) ingevoerd. We kunnen nu onmiddelijk aflezen dat de coördinaat van de top \((x_t,y_t)\) gelijk is aan
\begin{equation*} \boxed{ \left (x_t,y_t \right ) = \left (-\dfrac{b}{2a}, - \dfrac{D}{4a} \right)} \end{equation*}
Merk op dat je de formule voor de \(y\)-coördinaat van de top niet hoeft te memoriseren. Er geldt immers dat
\begin{equation*} \boxed{y_t = f(x_t) = f \left (-\frac{b}{2a} \right) } \end{equation*}

Voorbeeld 3.1.2. Functievoorschrift van een kwadratische functie bepalen.

Om het functievoorschrift van een kwadratische functie te bepalen heb je — in het algemeen geval — drie punten nodig. Als de top \((p,q)\) gegeven is, zijn twee punten echter voldoende.
Als voorbeeld bepalen we het functievoorschrift van de kwadratische functie \(f\) voorgesteld door nevenstaande grafiek. De top is \(\left ( -\dfrac{1}{2},2 \right ) \) dus we kunnen al schrijven dat
\begin{equation*} k(x)=a \left (x+\dfrac{1}{2} \right )^2 + 2 \end{equation*}
\(a\) bepalen we door het punt \(\left (\dfrac{1}{2},5 \right )\) in te vullen:
\begin{align*} \amp 5= a \left (\dfrac{1}{2}+\dfrac{1}{2} \right )^2 +2 \\ \Leftrightarrow \; \amp 5 = a + 2 \\ \Leftrightarrow \; \amp a = 3 \end{align*}
en het voorschrift is \(k(x) = 3 \left (x+\dfrac{1}{2} \right )^2 + 2\)

Subsectie 3.1.2 Van topvorm naar ontbonden vorm

Als de topvorm van een kwadratische functie gelijk is aan het verschil van twee kwadraten, dan kan die snel omgezet worden in de ontbonden vorm door te steunen op de identiteit
\begin{equation*} \boxed{a^2-b^2=(a-b)(a+b)} \end{equation*}
Bijvoorbeeld
\begin{align*} f(x)= \amp -2 (x+1)^2 + 18 \\ = \; \amp -2 \left [ (x+1)^2 -9 \right ] \\ = \; \amp -2 (x+1-3)(x+1+3) \\ = \; \amp -2 (x-2)(x+4) \end{align*}
Als de topvorm gelijk is aan de som van twee kwadraten, dan is een ontbinding niet mogelijk. Bijvoorbeeld:
\begin{equation*} x^2+2x+2=(x+1)^2+1 \end{equation*}
Merk op dat de corresponderende kwadratische vergelijking dan ook geen oplossingen heeft.
\begin{equation*} (x+1)^2+1 = 0 \Leftrightarrow (x+1)^2 = -1 \end{equation*}
Algemeen kunnen we stellen dat de topvorm verder kan ontbonden worden als \(D \gt 0\text{:}\)
\begin{align*} f(x) = \; \amp a \left (x+\dfrac{b}{2a} \right )^2 - \dfrac{D}{4a}\\ = \; \amp a \left [ \left (x+\dfrac{b}{2a} \right )^2 - \dfrac{D}{4a^2} \right ]\\ = \; \amp a \left (x+\dfrac{b}{2a} -\frac{\sqrt{D}}{2a}\right ) \left (x+\dfrac{b}{2a} + \frac{\sqrt{D}}{2a}\right ) \end{align*}

Subsectie 3.1.3 Nulwaarden en de ontbonden vorm

Nulwaarden en nulpunten.

\(a\) is een nulwaarde van de functie \(f\) als en slechts als \(f(a)=0\text{:}\)
\begin{equation*} a \text{ is een nulwaarde van } \; f \Leftrightarrow f(a)=0 \end{equation*}
Als \(a\) een nulwaarde is van \(f\text{,}\) dan noemen we \((a,0)\) een nulpunt.
De nulpunten van een functie \(f\) zijn dus de punten van de grafiek van \(f\) die op de \(x\)-as liggen en de nulwaarden van \(f\) zijn dan de \(x\)-coördinaten van die nulpunten.

Voorbeeld 3.1.3. Tekentabel van een kwadratische functie.

We beschouwen twee lineaire functies
\begin{gather*} l_1(x)=2x-1\\ l_2(x)=3x+5 \end{gather*}
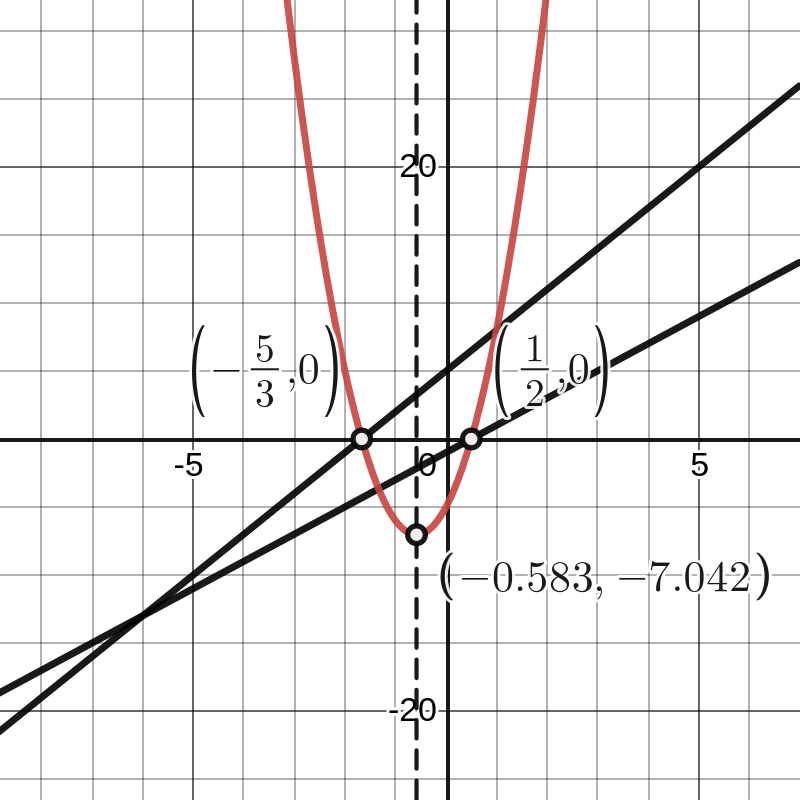
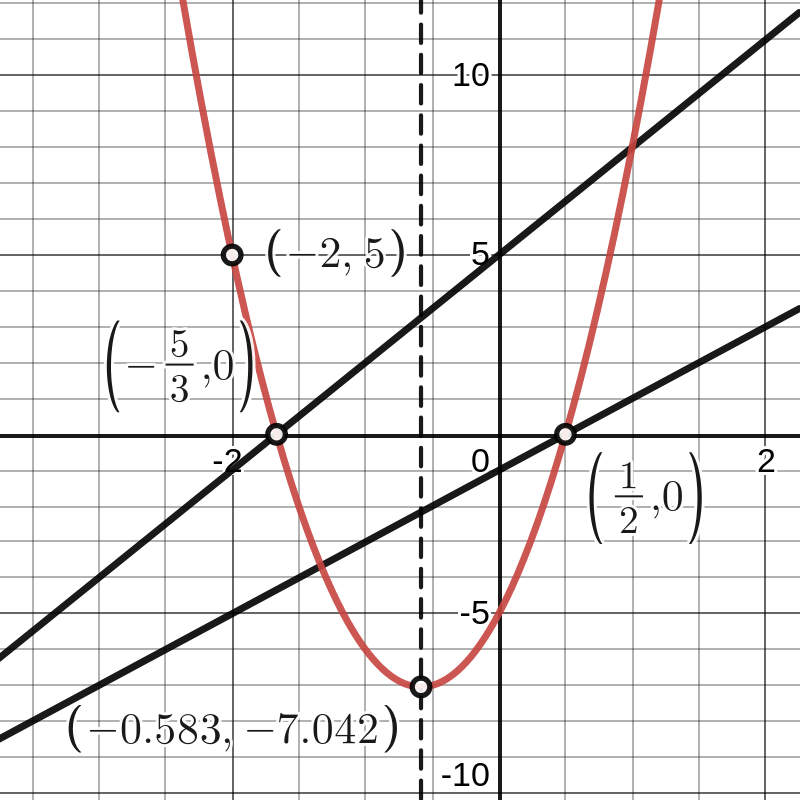
Het product van beide is de kwadratische functie \(k(x)=(2x-1)(3x+5)=6x^2+7x-5\text{.}\) We analyseren de ontbonden vorm even verder. De nulwaarden van de lineaire functies zijn
\begin{align*} \amp 2x-1=0 \quad \text{en} \amp \amp 3x+5=0\\ \Leftrightarrow \; \amp x=\frac{1}{2} \amp \Leftrightarrow \; \amp x=-\frac{5}{3} \end{align*}
Aangezien er geldt dat
\begin{equation*} a \cdot b = 0 \Leftrightarrow a=0 \quad \text{of} \quad b=0 \end{equation*}
kunnen we besluiten dat de nulwaarden van \(k\) gelijk zijn aan \(\dfrac{1}{2}\) en \(-\dfrac{5}{3}\text{.}\) Deze nulwaarden zijn gemakkelijk af te lezen als we het functievoorschrift als volgt herschrijven:
\begin{equation*} k(x)=(2x-1)(3x+5)=2 \left (x-\frac{1}{2} \right ) 3 \left (x+\dfrac{5}{3} \right )=6 \left (x-\frac{1}{2} \right ) \left (x+\dfrac{5}{3} \right ) \end{equation*}
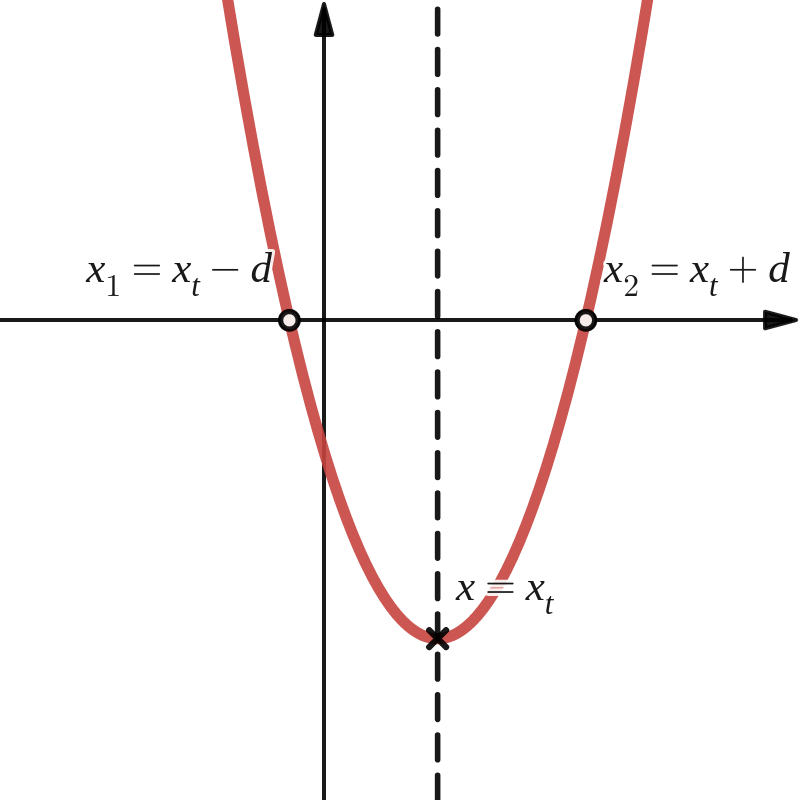
De positie van de symmetrie-as (en bijgevolg ook de \(x\)-coördinaat van de top) ligt in het midden van het lijnstuk bepaald door de nulwaarden. De tekentabel en het verloopschema van \(k(x)\) zien er dus als volgt uit:
Voor de volledigheid staan de tekentabellen van \(l_1(x)\) en \(l_2(x)\) er hierboven ook bij, maar uit het functievoorschrift van \(k(x)\) volgt eigenlijk onmiddellijk dat de grafiek een dalparabool is omdat \(6 \gt 0\text{.}\)
De ontbonden vorm
\begin{equation*} f(x) = a \left (x+\dfrac{b}{2a} -\frac{\sqrt{D}}{2a}\right ) \left (x+\dfrac{b}{2a} + \frac{\sqrt{D}}{2a}\right ) \end{equation*}
kan kort geschreven worden als
\begin{equation*} \boxed{f(x)=a(x-x_1)(x-x_2)} \end{equation*}
met
\begin{align*} \amp \boxed{x_1= - \dfrac{b}{2a} - \dfrac{\sqrt{D}}{2a}}\\ \amp \boxed{x_2= - \dfrac{b}{2a} + \dfrac{\sqrt{D}}{2a}} \end{align*}
de nulwaarden van \(f\text{.}\)

Ontbonden vorm van een kwadratische functie.

Een kwadratische functie \(f(x)=ax^2+bx+c\) met \(D \ge 0\) kan altijd geschreven worden als
\begin{equation*} f(x)=a(x-x_1)(x-x_2) \end{equation*}
met \(x_1\) en \(x_2\) de nulwaarden. De coördinaat van de top is \((x_t,f(x_t))\) met
\begin{equation*} x_t=\frac{x_1+x_2}{2} \end{equation*}
en de vergelijking van de symmetrie-as is \(x=x_t\text{.}\)

Voorbeeld 3.1.4. Functievoorschrift van een kwadratische functie bepalen.

We beschouwen dezelfde parabool als hierboven en bepalen het functievoorschrift op basis van de grafiek. De nulwaarden zijn gegeven, dus we kunnen al schrijven dat
\begin{equation*} k(x)=a \left (x+\dfrac{5}{3} \right ) \left (x-\dfrac{1}{2} \right) \end{equation*}
\(a\) bepalen we door het punt \((-2,5)\) in te vullen:
\begin{align*} \amp 5= a \left (-2+\dfrac{5}{3} \right ) \left (-2-\dfrac{1}{2} \right)\\ \Leftrightarrow \; \amp 5 = a \left (-\dfrac{1}{3} \right ) \left (-\dfrac{5}{2} \right ) \\ \Leftrightarrow \; \amp a = 6 \end{align*}

Subsectie 3.1.4 Kwadratische vergelijkingen oplossen

Het oplossen van een kwadratische vergelijking \(ax^2+bx+c=0\) is equivalent met het bepalen van de nulwaarden van de functie \(f(x)=ax^2+bx+c\text{.}\) Als we \(f(x)\) kunnen ontbinden zijn de oplossingen van de vergelijking \(f(x)=0\) dus gewoon af te lezen.
Om een algemene procedure te vinden om de oplossingen van een kwadratische functie te bepalen, veronderstellen we dat het functievoorschrift kan geschreven worden als het product van twee lineaire functies
 3 
Dit kan natuurlijk enkel als \(D \ge 0\text{,}\) maar die voorwaarde komen we tegen tijdens de afleiding.
:
\begin{equation*} ax^2+bx+c=a(x-x_1)(x-x_2) \end{equation*}
We delen deze vergelijking door \(a\) en stellen \(\frac{b}{a}=b'\) en \(\frac{c}{a}=c'\text{:}\)
\begin{equation*} x^2+b'x+c'=(x-x_1)(x-x_2) \end{equation*}
We werken het rechterlid uit en stellen de coëfficiënten van de gelijksoortige termen in het linker- en rechterlid aan elkaar gelijk:
\begin{align*} \amp x^2+b'x+c'=x^2-(x_1+x_2)x+x_1x_2\\ \Rightarrow \; \amp \begin{cases} x_1+x_2=-b'\\ x_1x_2=c' \end{cases} \end{align*}
Voor eenvoudige gevallen kunnen we op basis van deze twee vergelijkingen de oplossingen snel bepalen.

Voorbeeld 3.1.5.

\(x^2-7x+10=0\)
\begin{equation*} \begin{cases} x_1+x_2=7\\ x_1x_2=10 \end{cases} \end{equation*}
\(x_1=2\)\(x_2=5\text{.}\)
Als \(x_1\) en \(x_2\) niet onmiddellijk kunnen bepaald worden, redeneren we als volgt verder. Aangezien \(x_t=\dfrac{x_1+x_2}{2}\text{,}\) geldt er dat
\begin{equation*} x_t=-\dfrac{b'}{2} \end{equation*}
en de positie van de symmetrie-as kan bijgevolg snel bepaald worden. De nulpunten liggen symmetrisch ten opzichte van de symmetrie-as, dus we kunnen stellen dat \(x_1=x_t-d\) en \(x_2=x_t+d\text{,}\) waarbij \(d \) gelijk is aan de afstand van de nulpunten tot de symmetrie-as. Nu moeten we alleen nog \(d\) vinden om de vergelijking te kunnen oplossen. Hiervoor kunnen we \(x_1x_2=c'\) gebruiken:
\begin{align*} \amp (x_t-d)(x_t+d)=c' \\ \Rightarrow \; \amp x_t^2-d^2=c' \\ \Rightarrow \; \amp d^2=x_t^2-c' \end{align*}
Met de waarden van \(x_t\) en \(d\text{,}\) kunnen we dan \(x_1\) en \(x_2\) bepalen.

Voorbeeld 3.1.6.

\(x^2-7x+10=0\)
\begin{equation*} \begin{cases} x_t=\frac{7}{2}\\ d^2=\frac{49}{4}-10=\frac{9}{4} \end{cases} \end{equation*}
\(x_1=\frac{7}{2}-\frac{3}{2}=2\)\(x_2=\frac{7}{2}+\frac{3}{2}=5\text{.}\)
Als \(x_t^2-\frac{c}{a} \lt 0\text{,}\) dan is is \(d^2 \lt 0 \) (of \(D \lt 0\)) en heeft de vergelijking geen oplossing. Dit betekent dat ons uitgangspunt verkeerd was en de kwadratische functie niet kan ontbonden worden in twee lineaire factoren.
We kunnen de bovenstaande redenering in het volgende stappenplan gieten:

Oplossen van een kwadratische vergelijking.

Het oplossen van de kwadratische vergelijking \(ax^2+bx+c=0\) verloopt als volgt.
  1. Deel de vergelijking door \(a\text{.}\) Dit leidt tot
    \begin{equation*} x^2+b'x+c'=0 \end{equation*}
    waarbij \(\frac{b}{a}=b'\) en \(\frac{c}{a}=c'\text{.}\)
  2. Er geldt dat
    \begin{equation*} \begin{cases} x_1+x_2=-b'\\ x_1x_2=c' \end{cases} \end{equation*}
    Voor eenvoudige gevallen kunnen we op basis van deze twee vergelijkingen de oplossingen snel bepalen.
  3. Als de oplossingen niet onmiddellijk te bepalen zijn, bepaal dan eerst de symmetrie-as:
    \begin{equation*} x_t=-\frac{b'}{2} \end{equation*}
  4. Bepaal vervolgens \(d^2\text{:}\)
    \begin{equation*} d^2=x_t^2-c' \end{equation*}
  5. Als \(d^2 \lt 0\) heeft de vergelijking geen oplossingen. Als \(d^2 \ge 0\) zijn de oplossingen gelijk aan:
    \begin{equation*} x_1=x_t-d \quad \text{of} \quad x_2=x_t+d \end{equation*}

Opdracht 3.1.1.

Toon aan dat bovenstaand stappenplan leidt tot \(x=\dfrac{-b\pm \sqrt{D}}{2a}\) voor de oplossingen van de kwadratische vergelijking \(ax^2+bx+c=0\text{.}\)
Oplossing.
Er geldt dat \(x_t=-\dfrac{b'}{2}\) en \(d^2=x_t^2-c'\text{.}\) We substitueren \(b'=\dfrac{b}{a}\) en \(c'=\dfrac{c}{a}\text{:}\)
\begin{align*} \amp x_t=-\frac{b}{2a}\\ \amp d^2=\frac{b^2}{4a^2}-\frac{c}{a}=\frac{b^2-4ac}{4a^2}=\frac{D}{4a^2} \end{align*}
De oplossingen zijn
\begin{gather*} x_1=x_t-d=-\frac{b}{2a}-\frac{\sqrt{D}}{2a}\\ x_2=x_t+d=-\frac{b}{2a}+\frac{\sqrt{D}}{2a} \end{gather*}
VorigTopVolgend