Subsectie 4.1.1 Gemiddelde verandering
Gegeven de veeltermfunctie \(f(x)=x^3-x^2-x\text{.}\) Door het functievoorschrift te ontbinden
\begin{equation*}
f(x)=x \left (x - \frac{1-\sqrt{5}}{2} \right) \left (x - \frac{1+\sqrt{5}}{2} \right)
\end{equation*}
kunnen we onmiddellijk een tekentabel opstellen:
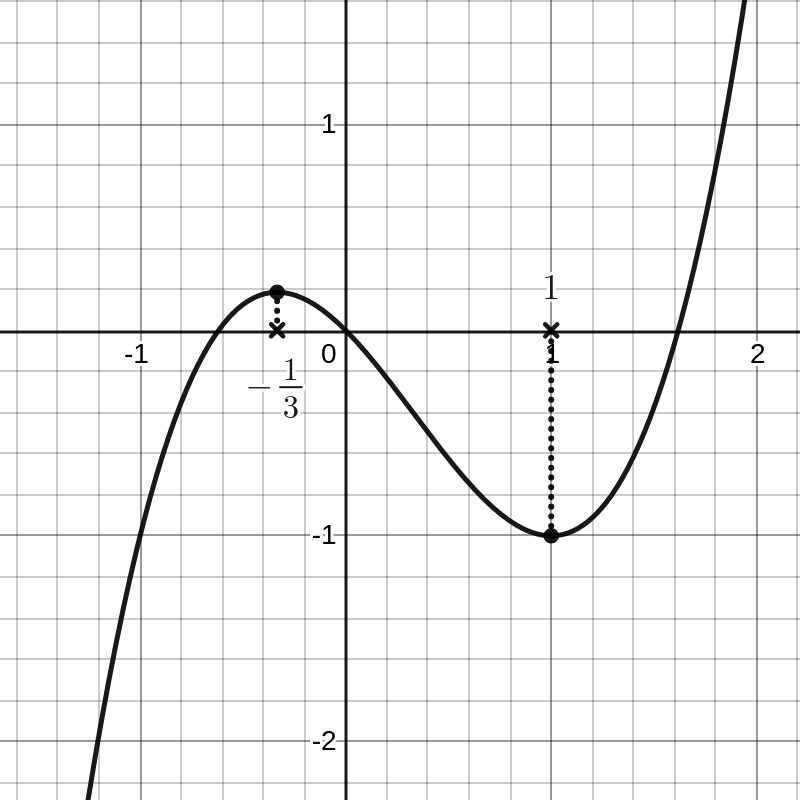
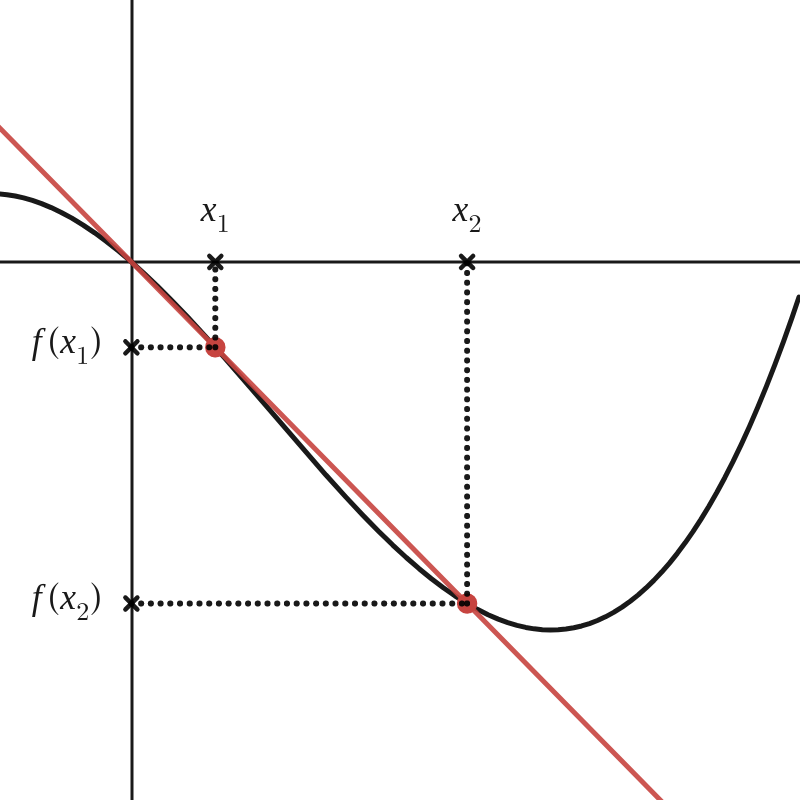
De tekentabel geeft ons in één oogopslag de nulwaarden van de functie en de intervallen waar de functiewaarden positief of negatief zijn. Het probleem dat we nu willen oplossen is het bepalen van de intervallen waar de functie stijgt of daalt, alsook de posities van de maxima en minima. Voor de gegeven functie lezen we op de grafiek af dat er een maximum is voor \(x=-\dfrac{1}{3}\) en een minimum voor \(x=1\text{;}\) dat de functie stijgt in \(\left ]-\infty,-\dfrac{1}{3} \right ] \cup \left [1,+\infty \right [\) en daalt in \(\left [-\dfrac{1}{3},1 \right ]\text{.}\)
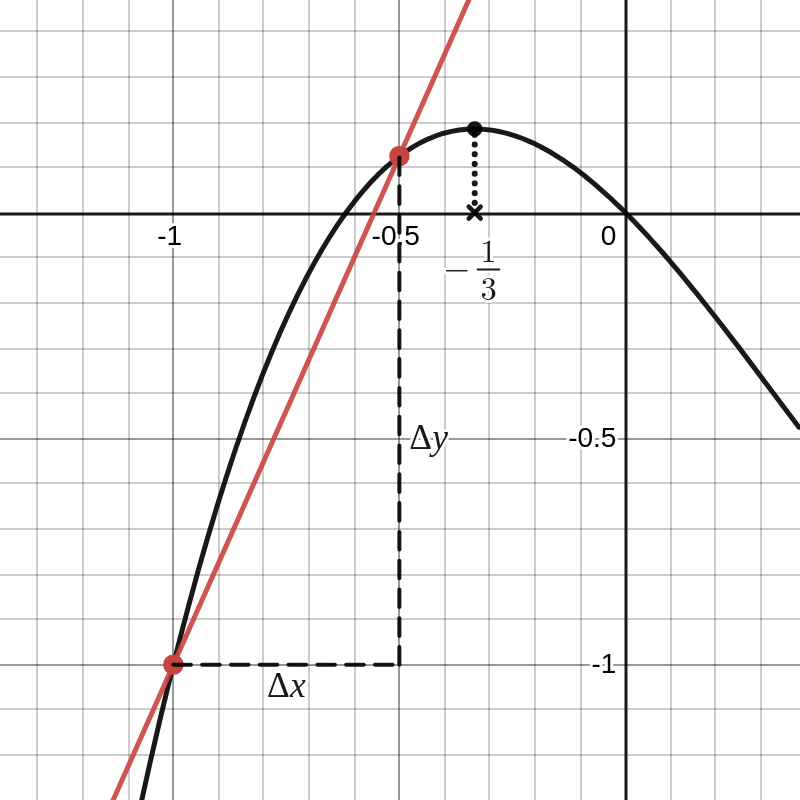
Veronderstel nu dat de grafiek van \(f\) de dwarsdoorsnede is van een — niet zo realistisch (we negeren bijvoorbeeld dat de functiewaarden oneindig groot of klein worden als \(x\) oneindig groot of klein wordt) — bergachtig landschap. Als je klimt van \(x=-1\) tot \(x=-0,5\) is je hoogteverschil \(f(-0,5)-f(-1)=1,125\text{.}\) We delen deze verticale toename door de horizontale toename:
\begin{equation*}
\frac{\Delta y}{\Delta x}=\frac{f(-0,5)-f(-1)}{0,5}=2,250
\end{equation*}
Voor elke kilometer (we nemen km als lengte-eenheid) die je horizontaal aflegt, klim je dus 2,25 km omhoog.
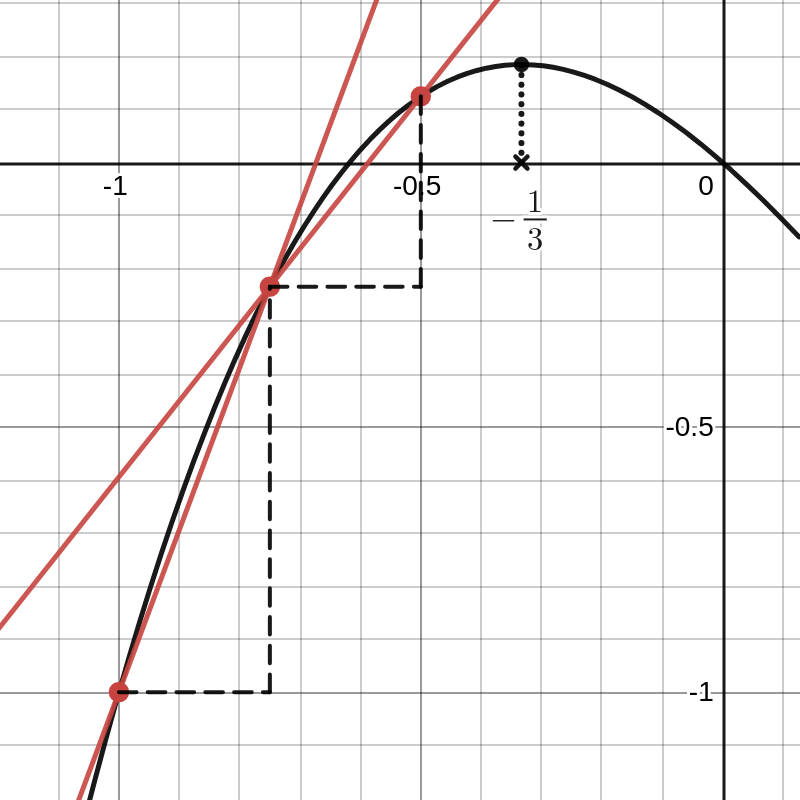
We noemen \(\dfrac{\Delta y}{\Delta x}\) de gemiddelde verandering van de functie \(f\) in het interval \(\Delta x\text{.}\) De klim is duidelijk steiler in de eerste helft van het interval. De gemiddelde verandering in het interval \([-1,-0,75]\) is
\begin{equation*}
\frac{\Delta y}{\Delta x}=\frac{f(-0,75)-f(-1)}{0,25}=3,063
\end{equation*}
en in het interval \([-0,75,-0,5]\)
\begin{equation*}
\frac{\Delta y}{\Delta x}=\frac{f(-0,5)-f(-0,75)}{0,25}=1,438
\end{equation*}
Opdracht 4.1.1.
Bereken de gemiddelde hellingshoek van \(f\) in
het interval \([-1,-0,75]\)
het interval \([-0,75,-0,5]\)
het interval \([-1,-0,5]\)
Oplossing.
\begin{equation*}
\tan \theta = 3,063 \Rightarrow \theta = \tan^{-1}(3,063)=71,9^{\circ}
\end{equation*}
\begin{equation*}
\tan \theta = 1,438 \Rightarrow \theta = \tan^{-1}(1,438)=55,2^{\circ}
\end{equation*}
\begin{equation*}
\tan \theta = 2,250 \Rightarrow \theta = \tan^{-1}(2,250)=66,0^{\circ}
\end{equation*}
Stijgen en dalen.
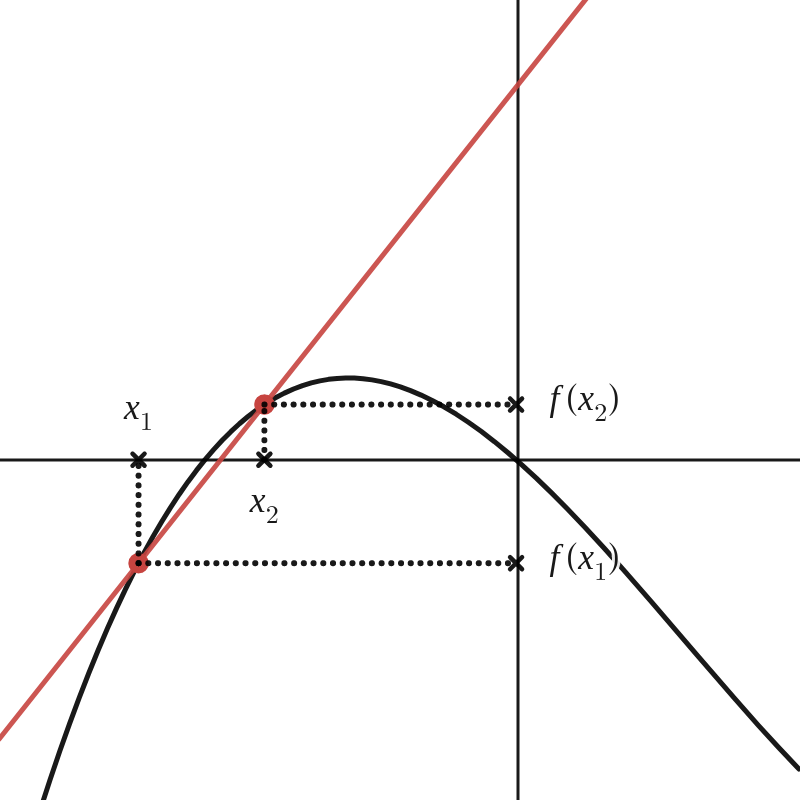
Een functie is strikt stijgend in een interval \([a,b]\) als en slechts als voor twee willekeurige punten \(x_1\) en \(x_2\) in het interval geldt dat de richtingscoëfficiënt van de rechte door de punten \((x_1,f(x_1))\) en \((x_2,f(x_2))\) strikt positief is.
\(f\) is strikt stijgend in \([a,b] \Leftrightarrow \forall x_1,x_2 \in [a,b] \text{ en } x_1 \neq x_2: \dfrac{f(x_2)-f(x_1)}{x_2-x_1} \gt 0 \)
Een functie is strikt dalend in een interval \([a,b]\) als en slechts als voor twee willekeurige punten \(x_1\) en \(x_2\) in het interval geldt dat de richtingscoëfficiënt van de rechte door de punten \((x_1,f(x_1))\) en \((x_2,f(x_2))\) strikt negatief is.
\(f\) is strikt dalend in \([a,b] \Leftrightarrow \forall x_1,x_2 \in [a,b] \text{ en } x_1 \neq x_2: \dfrac{f(x_2)-f(x_1)}{x_2-x_1} \lt 0 \)
Subsectie 4.1.2 Puntsgewijze verandering
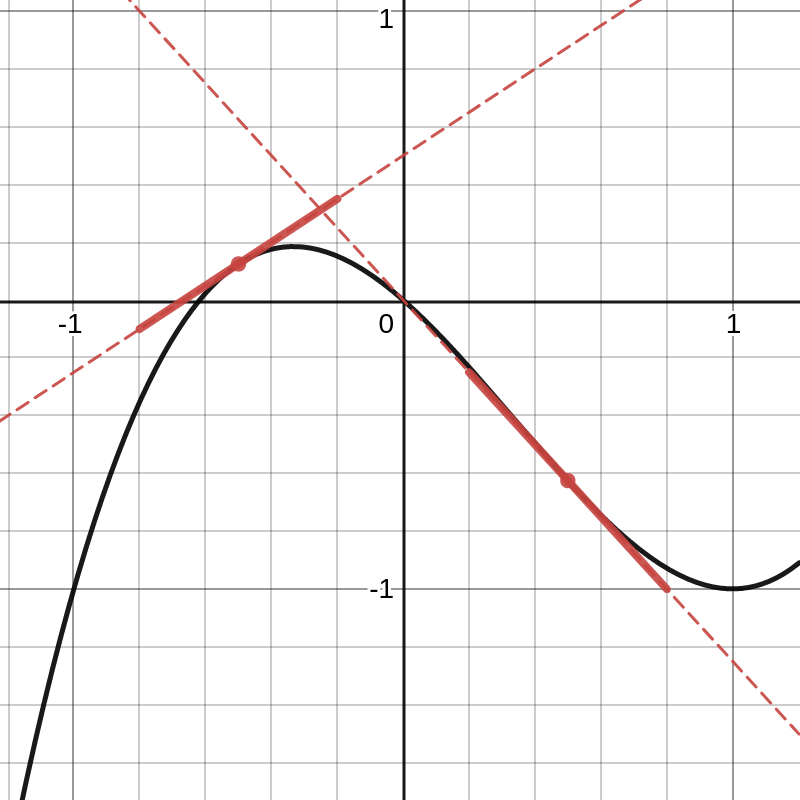
We willen nu de puntsgewijze verandering van de functie \(f\) bepalen. Bijvoorbeeld: “Hoe steil is de helling als \(x=-0,5\text{?}\)” Het is misschien wat vreemd om te spreken over de verandering in een punt, maar als je positie \(x=-0,5\) is, sta je wel duidelijk op een stijgende helling, terwijl de helling dalend is voor \(x=0,5\text{.}\) Stel je nu voor dat je in het punt \((-0,5;f(-0,5))\) en het punt \((0,5;f(0,5))\) een plank legt die dat punt (en enkel in dat punt) de grond raakt. De puntsgewijze verandering is dan de helling van de plank. Of wiskundig geformuleerd: de puntsgewijze verandering in een punt \((a,f(a))\) is de richtingscoëfficiënt van de raaklijn aan de grafiek van \(f\) in dit punt.
Het is wel niet onmiddellijk duidelijk hoe we de richtingscoëfficiënt van de raaklijn kunnen bepalen. In een punt is \(\Delta x = \Delta y = 0\) en we krijgen de onbepaalde vorm \(\dfrac{0}{0}\)
\begin{equation*}
\frac{\Delta y}{\Delta x}=\frac{0}{0}= \text{ ? }
\end{equation*}
We starten daarom met het bepalen van een benadering voor de puntsgewijze verandering in \(x=-0,5\) door de gemiddelde verandering \(\dfrac{\Delta y}{\Delta x}\) te berekenen in steeds kleiner wordende intervallen \(\Delta x\text{.}\) We ronden af op vijf cijfers na de komma en beginnen met \(\Delta x = 0,5\text{:}\)
Vanaf \(\Delta x=5 \cdot 10^{-7}\) blijft de puntsgewijze verandering gelijk aan de constante waarde \(0,75000\text{.}\) Aangezien rekenmachines en computers een eindige precisie hebben, kan een numerieke benadering voor een puntsgewijze verandering dus gewoon berekend worden door de gemiddelde verandering te berekenen met \(\Delta x\) klein genoeg. Om te begrijpen waarom de gemiddelde verandering gelijk blijft aan 0,75000 als \(\Delta x \le 5 \cdot 10^{-7}\text{,}\) berekenen we \(\dfrac{\Delta y}{\Delta x}\) in het interval \([-0,5;-0,5+\Delta x]\text{.}\) We bepalen eerst een uitdrukking voor \(\Delta y=f(x+\Delta x) - f(x)\) met \(f(x)=x^3-x^2-x\text{:}\)
\begin{align*}
\Delta y = \; \amp f(-0,5+\Delta x) - f(x)\\
= \; \amp (-0,5+\Delta x)^3 - (-0,5+\Delta x)^2 - (-0,5+\Delta x) - (-0,5)^3+(-0,5)^2 -0,5 \\
= \; \amp 0,75 \Delta x - 1,5 (\Delta x)^2 +(\Delta x)^3 + \Delta x -(\Delta x)^2 - \Delta x\\
= \; \amp 0,75 \Delta x - 2,5 (\Delta x)^2 +(\Delta x)^3
\end{align*}
Hieruit volgt voor de gemiddelde verandering
\begin{equation*}
\frac{\Delta y}{\Delta x} = 0,75 - 2,5 \Delta x +(\Delta x)^2
\end{equation*}
Hoe kleiner \(\Delta x\) wordt, hoe kleiner de tweede en de derde term worden t.o.v. de eerste term:
Vanaf \(\Delta x = 5 \cdot 10^{-15}\) is de som van de tweede term en de derde term gelijk aan de tweede term. Het is dan alsof je nul optelt bij de tweede term. Hetzelfde gebeurt vanaf \(\Delta x = 5 \cdot 10^{-17}\) voor de tweede en de eerste term: de tweede term wordt zo klein t.o.v. de eerste term dat je eigenlijk gewoon nul aftrekt van 0,75. Dit komt natuurlijk omdat een computer maar een eindig aantal bits gebruikt om getallen voor te stellen. Als je met een computer de som \(a+b\) wil berekenen en \(b\) is ongeveer \(10^{16}\) keer kleiner dan \(a\text{,}\) dan tel je eigenlijk gewoon nul op bij \(a\text{.}\)
Opdracht 4.1.2.
Onderzoek hoe klein een getal \(\epsilon\) mag zijn vooraleer je rekenmachine zegt dat de som \(1+\epsilon = 1+0 \text{.}\)
Opdracht 4.1.3.
Als we de rechtstreekse berekening van \(\dfrac{\Delta y}{\Delta x}\) verder zetten voor kleinere \(\Delta x\) en het resultaat met meer precisie weergeven, zien we dat het resultaat gaat afwijken van 0,75 en uiteindelijk zelfs gelijk wordt aan nul. Verklaar! Pas gerust de code aan om je verklaring te controleren.
Oplossing.
Het verschil \(f(0,5+\Delta x)-f(0,5)\) wordt steeds kleiner en het resultaat onnauwkeuriger. Voor \(\Delta x = 5 \cdot 10^{-13}\) is \(f(0,5+\Delta x) = 0.125000000000375\) en \(f(0,5)=0.125000000000000\text{.}\) Het verschil heeft dus slechts 3 beduidende cijfers.
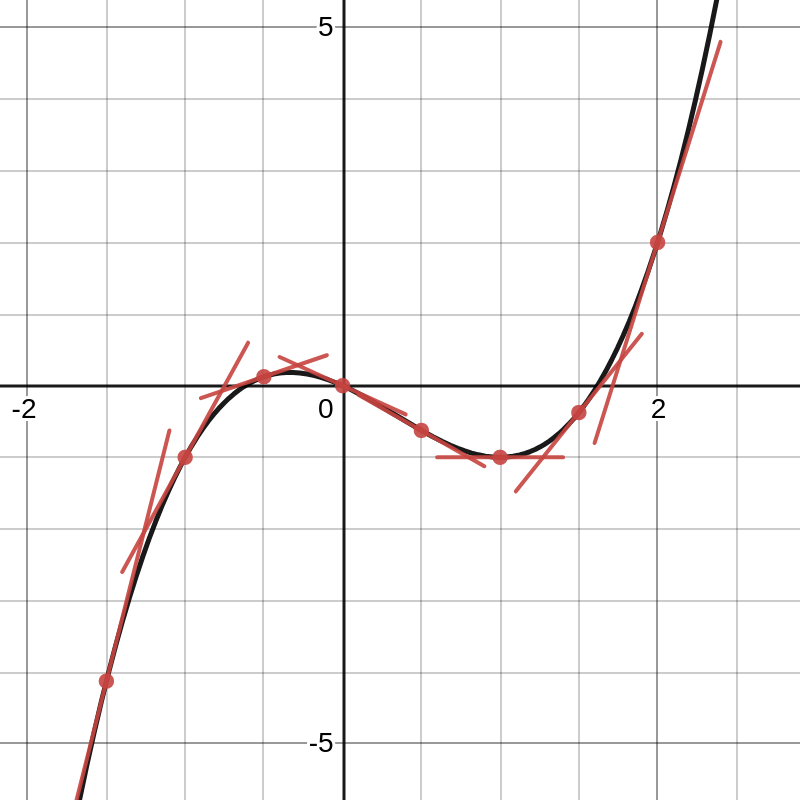
We kunnen dus in gelijk welk punt een numerieke benadering voor de puntsgewijze verandering bepalen door de gemiddelde verandering te berekenen voor een tijdsinterval \(\Delta x\) dat klein genoeg is. Onderstaande tabel toont in enkele punten de verandering tot twee cijfers na de komma nauwkeurig. Denk eraan dat die veranderingen de richtingscoëfficiënten zijn van de raaklijnen aan de grafiek.
Strikt positieve veranderingen corresponderen met strikt stijgende raaklijnen.
Strikt negatieve veranderingen corresponderen met strikt dalende raaklijnen.
Hoe groter de absolute waarde van de verandering, hoe steiler de raaklijn.
Als de verandering gelijk is aan nul, is de raaklijn horizontaal. Dit geldt voor de raaklijn in \(x=1\text{.}\) De functie bereikt daar een minimum.
| \(a\) |
\(\frac{\Delta y}{\Delta x}\) in \(a\)
|
| \(-1,50\) |
\(8,75\) |
| \(-1,00\) |
\(4,00\) |
| \(-0,50\) |
\(0,75\) |
| \(0,00\) |
\(-1,00\) |
| \(0,50\) |
\(-1,25\) |
| \(1,00\) |
\(0,00\) |
| \(1,50\) |
\(2,75\) |
| \(2,00\) |
\(7,00\) |
Opdracht 4.1.4.
Reken de waarden uit bovenstaande tabel na. Gebruik hiervoor onderstaande code.
Als we de waarden uit bovenstaande tabel in een grafiek uitzetten, dan merken we dat deze punten op de grafiek liggen van een parabool met vergelijking
\(y=3x^2-2x-1\text{.}\) (Desmos link)www.desmos.com/calculator/uynl4puqwb
:
De puntsgewijze verandering van de functie \(f(x)=x^3-x^2-x\) wordt dus blijkbaar gegeven door een functie \(g\) met voorschrift \(g(x)=3x^2-2x-1\text{.}\) Dit betekent dat in elk punt \((a,f(a))\) van de grafiek van \(f\) de vergelijking van de raaklijn gegeven wordt door
\begin{equation*}
y=g(a)(x-a)+f(a)
\end{equation*}
Nu rest ons enkel nog het expliciet opstellen van het functievoorschrift \(g(x)\text{.}\) In een willekeurig punt \(x\) is de verticale verandering \(\Delta y\) gelijk aan
\begin{align*}
\Delta y = \; \amp f(x+\Delta x) - f(x)\\
= \; \amp (x+\Delta x)^3 - (x+\Delta x)^2 - (x+\Delta x) - x^3+x^2 + x \\
= \; \amp 3x^2 \Delta x + 3x (\Delta x)^2 + (\Delta x)^3 - 2x \Delta x - (\Delta x)^2 - \Delta x\\
= \; \amp (3x^2-2x-1) \Delta x + (3x-1) (\Delta x)^2 + (\Delta x)^3
\end{align*}
De gemiddelde verandering in het interval \(\Delta x\) is dus
\begin{equation*}
\frac{\Delta y}{\Delta x} = (3x^2-2x-1) + (3x-1) (\Delta x) + (\Delta x)^2
\end{equation*}
Door \(\Delta x\) kleiner en kleiner te maken, zal \(\frac{\Delta y}{\Delta x} \) naderen tot \(3x^2-2x-1\) omdat de termen die \(\Delta x\) als een factor bevatten, klein worden t.o.v. termen zonder \(\Delta x\text{.}\) We noteren (lees: de limiet voor \(\Delta x \to 0\))
\begin{align*}
\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \; \amp \lim_{\Delta x \to 0} \left ( (3x^2-2x-1) + (3x-1) (\Delta x) + (\Delta x)^2 \right ) \\
= \; \amp 3x^2-2x-1
\end{align*}
Opmerking 4.1.1.
Aangezien \(\Delta x \to 0\) een proces is dat nooit eindigt (er is immers geen kleinste reëel getal), wordt \(\dfrac{\Delta y}{\Delta x}\) eigenlijk nooit exact gelijk aan \(3x^2-2x-1\text{.}\)
Opdracht 4.1.5.
Gegeven de functie \(f(x) = -x^2+4x+5\)
-
Bepaal de puntsgewijze verandering van \(f\) in \(x =-2\text{,}\) \(x = 0\) en \(x = 3\text{.}\)
Plot deze puntsgewijze veranderingen in Desmos en controleer dat ze op de rechte met vergelijking \(y=-2x+4\) liggen.
Teken in Desmos de grafiek van \(f\) en de raaklijnen in de punten \((-2,-7)\text{,}\) \((0,5)\) en \((3,8)\) aan de grafiek.
Toon aan dat de puntsgewijze verandering van \(f\) in een willekeurig punt \(x\) gegeven wordt door \(g(x)=-2x+4\) door \(\displaystyle \lim_{x \to 0} \frac{\Delta y}{\Delta x} \) te berekenen.
Oplossing.
De puntsgewijze veranderingen zijn respectievelijk
\(8\text{,}\) \(4\) en
\(-2\text{.}\) Zie
hierwww.desmos.com/calculator/gwdame1bgy
voor de oplossing van 2 en 3. Puntje 4 staat uitgeschreven op Smartschool.
Afgeleide functie.
De afgeleide functie \(f'\) van een gegeven reële functie \(f\) is de functie die \(x\) afbeeldt op \(f'(x)\) met \(f'(x)\) de puntsgewijze verandering van \(f\) in \(x\text{.}\) Praktisch bepaal je \(f'(x)\) als volgt:
Werk \(\Delta y = f(x+\Delta x) - f(x)\) uit en vereenvoudig zoveel mogelijk.
Deel \(\Delta y\) door \(\Delta x\text{.}\)
Door \(\Delta x\) vervolgens gelijk te stellen aan nul, krijg je de puntsgewijze verandering \(f'(x)\) in \(x\text{.}\)
Deze praktische berekening noteer je kort als
\begin{equation*}
f'(x)=\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}
\end{equation*}
Een exacte definitie van het begrip limiet stellen we voorlopig uit omdat die vrij technisch is. Het intuïtieve idee achter deze notatie, zoals uiteengezet in deze paragraaf, is voldoende om met afgeleide functies aan de slag te gaan.
De afgeleide functie wordt op verschillende manieren genoteerd:
\begin{equation*}
f' \qquad \text{of} \qquad \frac{df}{dx} \qquad \text{of} \qquad Df
\end{equation*}
\begin{equation*}
f'(x) \qquad \text{of} \qquad \frac{df(x)}{dx} \qquad \text{of} \qquad Df(x)
\end{equation*}
De notaties worden door elkaar gebruikt zodat je eraan went.
Opmerking 4.1.2.
We zijn er tot nog toe altijd van uitgegaan dat \(\Delta x \gt 0\text{,}\) maar we kunnen even goed een stapje terug zetten. Bovenstaande redeneringen blijven gelden voor \(\Delta x \lt 0\text{.}\)
Meetkundige betekenis van \(f'(a)\).
\(f'(a)\) is de richtingscoëfficiënt van de raaklijn aan de grafiek van \(f\) in het punt \((a,f(a))\text{.}\) Dit betekent dat de vergelijking van de raaklijn gegeven wordt door:
\begin{equation*}
y=f'(a)(x-a)+f(a)
\end{equation*}