Definitie 2.6.1.
Een functie \(f\) met voorschrift
\begin{equation*}
f(x)=\frac{ax+b}{cx+d} \qquad \text{met } c \neq 0 \text{ en } ad \neq bc
\end{equation*}
noemen we een homografische functie.
Sectie 2.6 Homografische functies
In Verkenning 2.3.1 heb je het quotiënt van twee lineaire functies onderzocht en normaal gezien gemerkt dat de grafiek een hyperbool voorstelt.
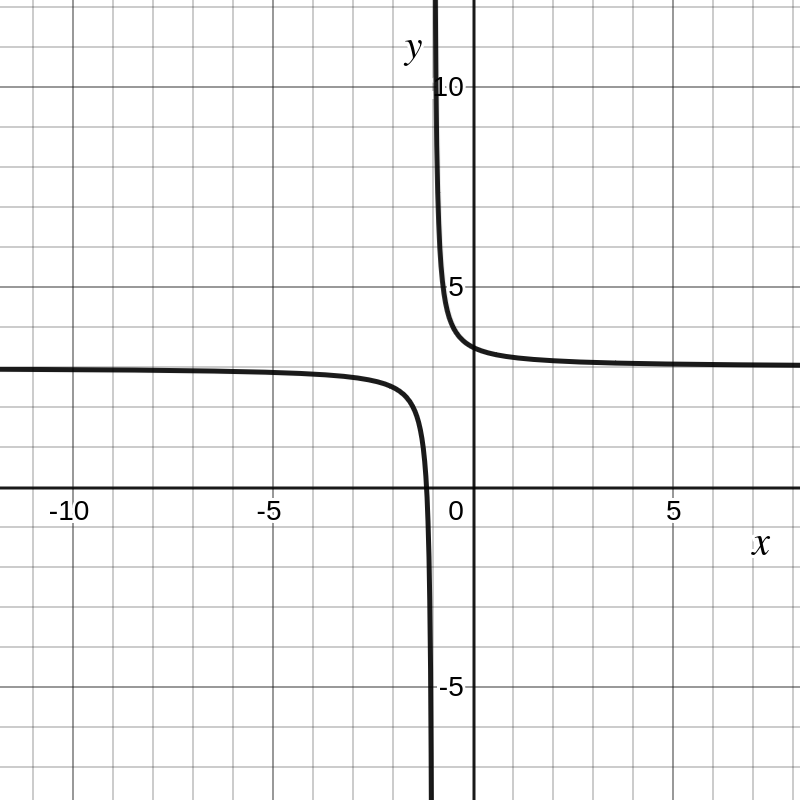
Als voorbeeld bekijken we de functie \(f(x)=\dfrac{6x+7}{2x+2}\) voorgesteld door onderstaande grafiek
Uit de grafiek volgt onmiddellijk dat het functievoorschrift ook in de vorm
\begin{equation*}
f(x) = a \dfrac{1}{x+1} + 3
\end{equation*}
kan geschreven worden. Om dit aan te tonen, voeren we de deling \(\dfrac{6x+7}{2x+2}\) uit. Dat gaat als volgt:
1
Vergelijk met \(\dfrac{7}{2} = \dfrac{3 \cdot 2 +1}{2} = 3 + \dfrac{1}{2}\)
\begin{align*}
\frac{6x+7}{2x+2} = \; \amp \frac{3 (2x+2) +1}{2x+2} \\
= \; \amp 3 + \frac{1}{2x+2} \\
= \; \amp \frac{1}{2} \frac{1}{x+1} + 3
\end{align*}
Definitie 2.6.2.
Een rechte is een asymptoot van de grafiek van een functie als de afstand tussen de grafiek van de functie en de rechte steeds kleiner wordt.
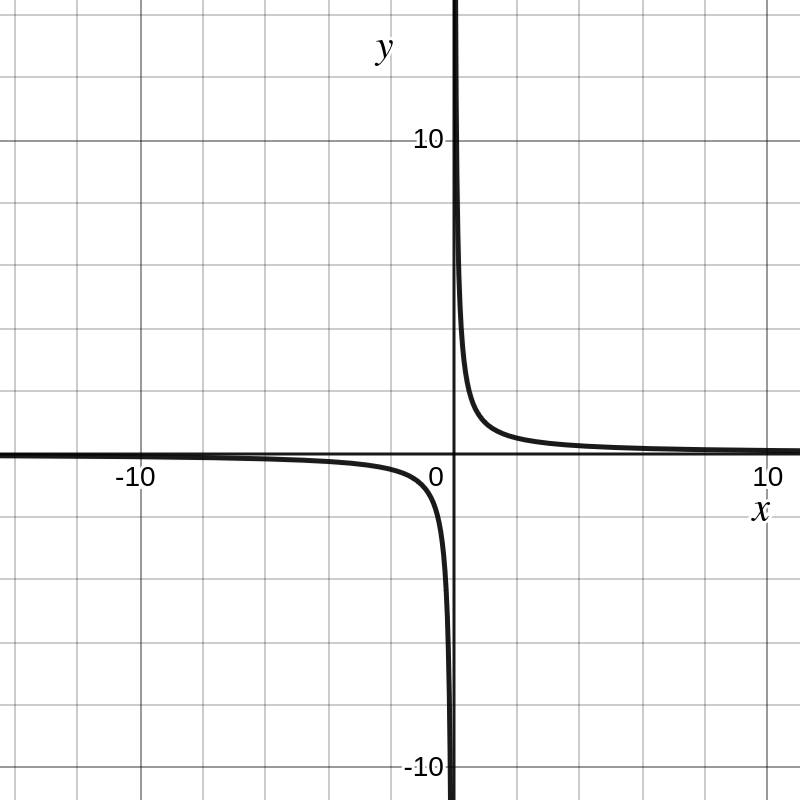
De grafiek van de functie \(g(x)=\dfrac{1}{x}\) heeft twee asymptoten:
- \(y=0\) is een horizontale asymptoot omdat \(f(x) \to 0\) als \(x \to \pm \infty\text{.}\) We noteren dit als \(\displaystyle \lim_{x \to \pm \infty} f(x) = 0\text{.}\)
- \(x=0\) is een verticale asymptoot omdat \(f(x) \to +\infty\) als \(x \to 0+\) en \(f(x) \to -\infty\) als \(x \to 0-\text{.}\) We noteren dit als \(\displaystyle \lim_{x \to 0+} f(x) = +\infty\) en \(\displaystyle \lim_{x \to 0-} f(x) = -\infty\text{.}\)
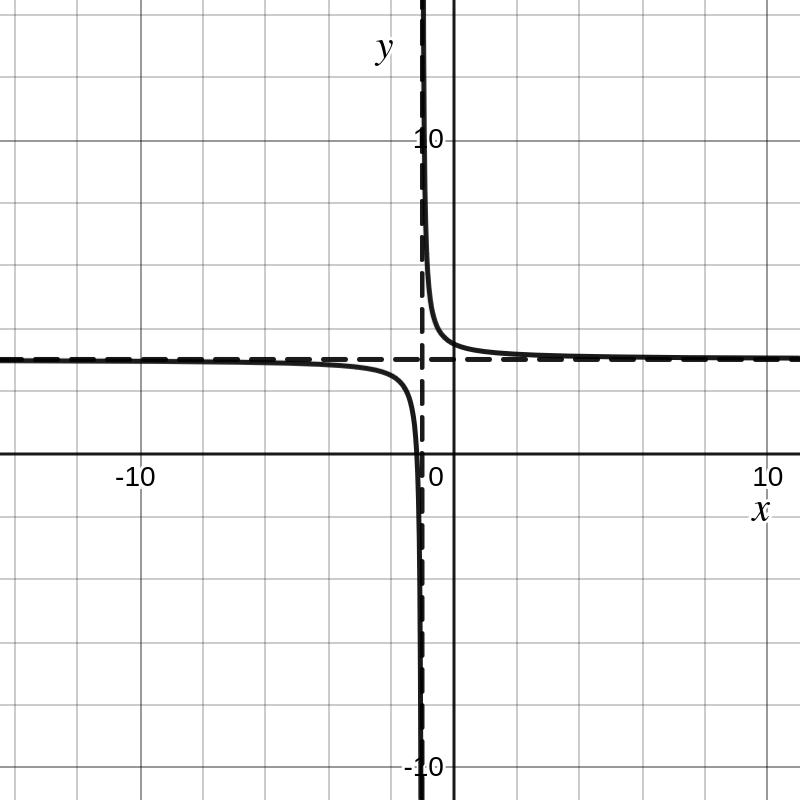
Dit betekent dat de grafiek van de functie \(f(x) = \dfrac{1}{2} \dfrac{1}{x+1} + 3\)
- een horizontale asymptoot \(y=3\) heeft (\(\displaystyle \lim_{x \to \pm \infty} f(x) = 3\)) en
- een verticale asymptoot \(x=-1\) \(\displaystyle \lim_{x \to (-1)+} f(x) = +\infty\) en \(\displaystyle \lim_{x \to (-1)-} f(x) = -\infty\)
Merk op dat natuurlijk \(\text{dom} f = \mathbb{R} \setminus \lbrace -1 \rbrace \) en \(\text{ber} f = \mathbb{R} \setminus \lbrace 3 \rbrace \text{.}\)
Eigenschappen van de homografische functie.
Door de deling uit te voeren kan elke homografische functie geschreven worden in de vorm
\begin{equation*}
f(x)=\dfrac{r}{x-p} + q
\end{equation*}
Hieruit volgt onmiddellijk dat dom \(f = \mathbb{R} \setminus \lbrace p \rbrace \) en ber \(f = \mathbb{R} \setminus \lbrace q \rbrace \text{.}\) De grafiek van \(f\) ontstaat uit de grafiek van \(y=\dfrac{1}{x}\) na de volgende transformaties
- verschuiven langs de \(x\)-as met \(p\) eenheden naar rechts (\(p \gt 0\)) of naar links (\(p \lt 0\));
- herschalen met factor \(r\) volgens de \(y\)-as
- verschuiven langs de \(y\)-as met \(q\) eenheden omhoog (\(q \gt 0\)) of omlaag (\(q \lt 0\));
\(y=q\) is een horizontale aymptoot en \(x=r \) een verticale asymptoot van de grafiek van \(f\text{.}\)
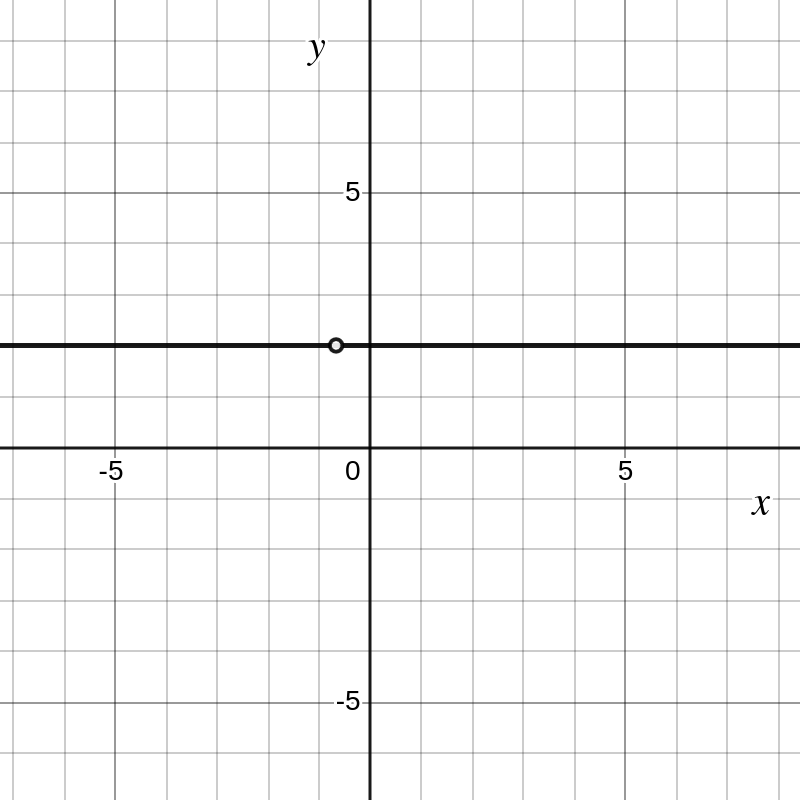
Voorbeeld 2.6.3. Horizontale rechte met een gat.
Als \(ad = bc\) is \(f(x)=\dfrac{ax+b}{cx+d} \) geen homografische functie. Beschouw bijvoorbeeld de functie \(f(x)=\dfrac{6x+4}{3x+2}\text{.}\) Door in de teller een factor twee voorop te zetten krijgen we
\begin{equation*}
f(x)= 2 \frac{3x+2}{3x+2} = 2 \qquad \text{als } x \neq -\frac{2}{3}
\end{equation*}
De grafiek is een horizontale rechte met een gat (dom \(f = \mathbb{R} \setminus \lbrace -\dfrac{2}{3} \rbrace\))
