Sectie 2.5 Transformaties van grafieken
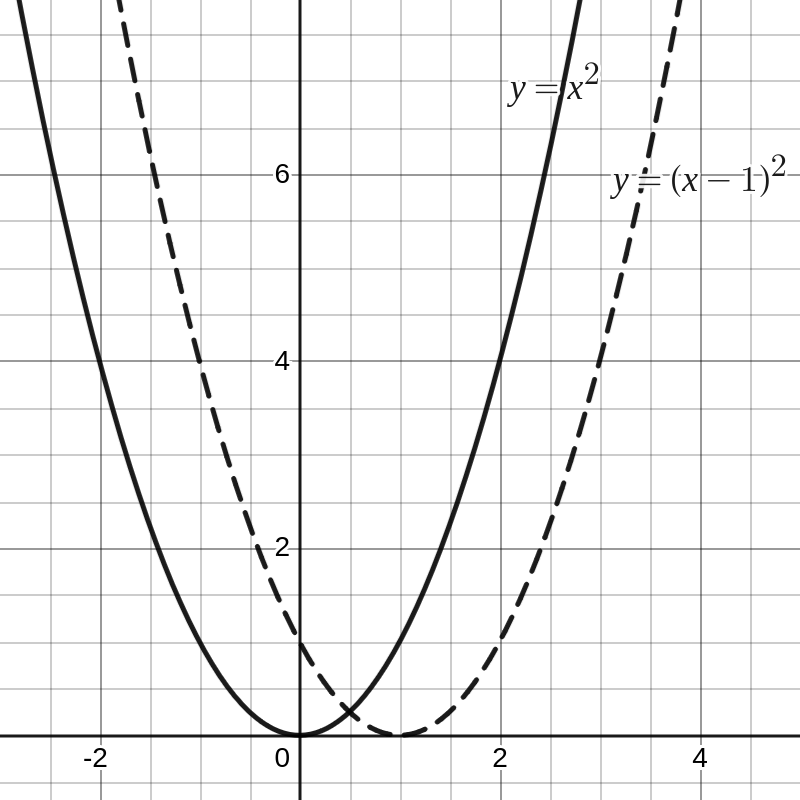
Je kan de grafiek van een functie altijd tekenen door voldoende functiewaarden te berekenen, maar er bestaan efficiëntere methoden. Beschouw bijvoorbeeld de functie \(f(x)=(x-1)^2\text{.}\) Als je weet dat de grafiek van \(y=x^2\) een parabool is en dat het effect van \(x\) vervangen door \(x-1\) neerkomt op het verschuiven van die parabool met één eenheid naar rechts, dan kan je heel snel de grafiek schetsen.
Onderstaande tabel geeft een overzicht van de mogelijke aanpassingen van het functievoorschrift van
\(f\) en de corresponderende transformaties van de grafiek van
\(f\text{.}\) Via
deze link kan je zelf experimenteren. Probeer zeker te begrijpen waarom elke aanpassing leidt tot de gegeven transformatie!
| aanpassing van \(f(x)\)
|
transformatie van grafiek |
|
\(x\) vervangen door \(x-a\)
|
verschuiven volgens \(x\)-as met \(a\) eenheden naar rechts |
|
\(x\) vervangen door \(x+a\)
|
verschuiven volgens \(x\)-as met \(a\) eenheden naar links |
|
\(f(x)\) vervangen door \(f(x)+a\)
|
verschuiven volgens \(y\)-as met \(a\) eenheden naar boven |
|
\(f(x)\) vervangen door \(f(x)-a\)
|
verschuiven volgens \(y\)-as met \(a\) eenheden naar beneden |
|
\(x\) vervangen door \(a \cdot x\)
|
herschalen volgens \(x\)-as met factor \(\dfrac{1}{a}\)
|
|
\(f(x)\) vervangen door \(a \cdot f(x)\)
|
herschalen volgens \(y\)-as met factor \(a\)
|
|
\(x\) vervangen door \(-x\)
|
spiegelen om de \(y\)-as |
|
\(f(x)\) vervangen door \(-f(x)\)
|
spiegelen om de \(x\)-as |
Als je verschillende transformaties na elkaar toepast, dan hangt het eindresultaat af van de volgorde van de transformaties. Beschouw bijvoorbeeld de lineaire functie \(f(x)=x\) en de volgende transformaties van de grafiek
herschalen met een factor 2 volgens de \(y\)-as
3 eenheden omlaag schuiven volgens de \(y\)-as
1 eenheid naar links schuiven volgens de \(x\)-as
Het eindresultaat is dan de grafiek van de functie \(f_1(x)=2(x+1)-3\text{.}\) Veranderen we echter de volgorde in
1 eenheid naar links schuiven volgens de \(x\)-as
3 eenheden omlaag schuiven volgens de \(y\)-as
herschalen met een factor 2 volgens de \(y\)-as
dan is het eindresultaat de grafiek van de functie \(f_2(x)=2(x+1-3)=2x-4\)
Bovenstaande transformaties zijn ook niet de enige manier om de grafiek van \(f\) te transformeren in de grafiek van \(f_1(x)\text{.}\) Werken we het functievoorschrift uit
\begin{equation*}
f_1(x)=2(x+1)-3=2x-1
\end{equation*}
dan zien we dat
herschalen met een factor 2 volgens de \(y\)-as
1 eenheid omlaag schuiven volgens de \(y\)-as
eveneens de grafiek van \(f\) omzet in de grafiek van \(f_1\text{.}\) We kunnen ook schrijven dat
\begin{equation*}
f_1(x)=2x-1=2 \left (x-\dfrac{1}{2} \right )
\end{equation*}
en bijgevolg transformeren
1/2 eenheid naar rechts schuiven volgens de \(x\)-as
herschalen met een factor 2 volgens de \(y\)-as
ook de grafiek van \(f\) in die van \(f_1\text{.}\)
Je zal waarschijnlijk al wel door hebben dat het transformeren van grafieken kan gelinkt worden aan het samenstellen van functies. Beschouw bijvoorbeeld de kwadratische functie \(f(x)=x^2\) en de functie \(g_1(x)=x+2\text{.}\) Er geldt dan dat
\begin{gather*}
(g_1 \circ f)(x) = g_1(f(x))=x^2+2\\
(f \circ g_1)(x) = f(g_1(x))=(x+2)^2
\end{gather*}
Het effect van de eerste samenstelling is een verschuiving van de parabool naar boven met twee eenheden; de tweede samenstelling verschuift de parabool naar links met twee eenheden.
De grafiek van een samengestelde functie kan stapsgewijs geschetst worden door elke stap van de samenstelling te tekenen, vertrekkende van de rechte \(y=x\text{.}\) We passen dit toe op \((g_1 \circ f)(x) = x^2+2\text{:}\)
We starten met het tekenen van de rechte \(y=x\text{.}\)
De eerste functie in de samenstelling is \(f(x)\text{,}\) dus we kwadrateren alle \(y\)-coördinaten van de punten op de rechte en krijgen de parabool \(y=x^2\text{.}\)
Vervolgens passen we de functie \(g_1\) toe. Dit betekent dat we twee optellen bij de \(y\)-coördinaten van de punten van de parabool en de parabool verschuift met twee eenheden omhoog.
We herhalen bovenstaande procedure voor \((f \circ g_1)(x) =(x+2)^2\text{:}\)
We starten met het tekenen van de rechte \(y=x\text{.}\)
De eerste functie is nu \(g_1\text{,}\) dus we tellen twee op bij de \(y\)-coördinaten van de punten van de rechte. De rechte verschuift naar boven met twee eenheden. Merk op dat dit equivalent is met een verschuiving naar links met twee eenheden.
Vervolgens passen we de functie \(f\) toe en kwadrateren we alle \(y\)-coördinaten van de punten op de rechte. We krijgen dan de grafiek van de parabool \(y=(x+2)^2\text{.}\)
We bekijken nu het samenstellen met de functie \(g_2(x)=2x\text{:}\)
\begin{gather*}
(g_2 \circ f)(x) = g_2(f(x))=2x^2\\
(f \circ g_2)(x) = f(g_2(x))=(2x)^2
\end{gather*}
Het effect van de eerste samenstelling is een herschaling van de parabool met een factor 2 volgens de \(y\)-as; de tweede samenstelling is een herschaling met factor \(\dfrac{1}{2}\) volgens de \(x\)-as. We tonen dit opnieuw aan door de samenstellingen uit te schrijven en de grafiek stapsgewijs te tekenen. We beperken het domein van \(f\) om het verschil tussen herschalen volgens \(x\) of \(y\) duidelijk te maken.
Voorbeeld 2.5.1. Schetsen van de grafiek van een samengestelde functie.
We bekijken nu een moeilijker voorbeeld:
\begin{equation*}
f(x)=\sqrt{3x+6}
\end{equation*}
We gaan stap voor stap door de samenstelling en tekenen telkens de grafiek.
We starten altijd met de rechte \(y=x\text{.}\)
-
De eerste functie is \(f_1(x)=3x\text{,}\) dus we vermenigvuldigen de \(y\)-coördinaten van alle punten van de rechte met \(3\text{.}\) We krijgen dus een tweede rechte \(y=3x\text{.}\)
-
De volgende functie in de samenstelling is \(f_2(x)=x+6\text{.}\) De \(y\)-coördinaten van alle punten nemen nu met 6 toe en we gaan van de rechte \(y=3x \) naar de rechte \(y=3x+6\text{.}\)
-
Tenslotte nemen we de vierkantswortel van alle \(y\)-coördinaten en gaan we van de rechte \(y=3x+6\) naar de grafiek van de functie \(f(x)=\sqrt{3x+6}\text{.}\)
Als we de grafiek van \(f(x)=\sqrt{3x+6}\) vergelijken met de grafiek van \(y=\sqrt{x}\text{,}\) dan zien we dat deze twee eenheden naar links verschoven is en herschaald is met een factor \(\sqrt{3}\) volgens de \(y\)-as. Dit kan natuurlijk ook rechtstreeks uit het functievoorschrift afgeleid worden:
\begin{equation*}
f(x)=\sqrt{3x+6}=\sqrt{3(x+2)}=\sqrt{3} \cdot \sqrt{x+2}
\end{equation*}
Voorbeeld 2.5.2. Functievoorschrift bepalen op basis van de grafiek.
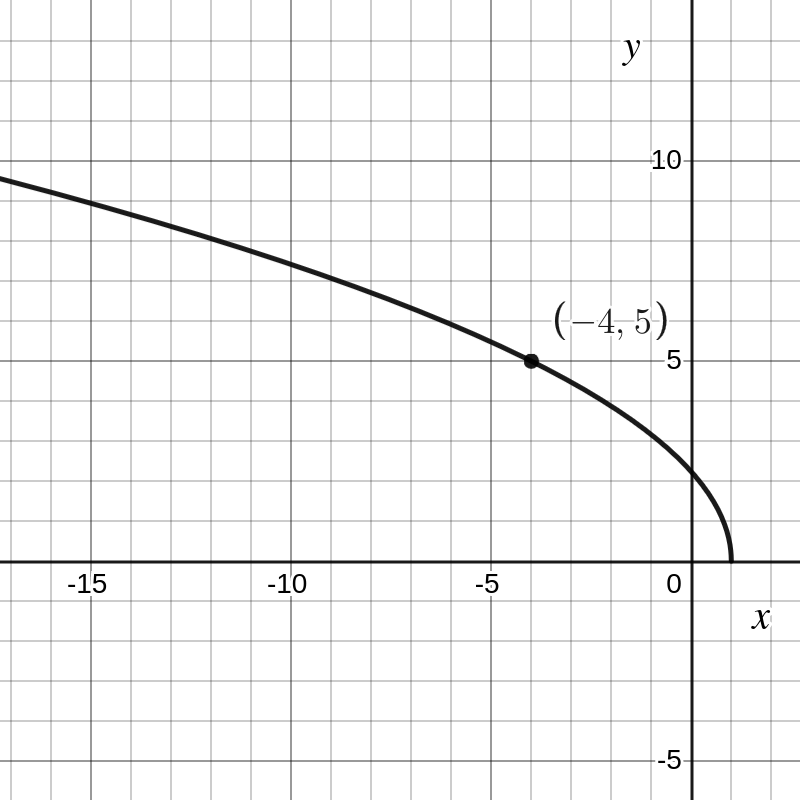
Stel dat je het functievoorschrift wil bepalen van de functie voorgesteld door onderstaande grafiek:
Het is onmiddelijk duidelijk dat dit de grafiek is van \(\sqrt{x}\) na de volgende transformaties
spiegelen om de \(y\)-as
verschuiven volgens de \(x\)-as naar rechts met één eenheid
herschalen volgens de \(y\)-as met een nog te bepalen factor \(a\)
Het voorschrift is dus van de vorm
\begin{equation*}
f(x)=a \sqrt{-(x-1)}
\end{equation*}
en de parameter \(a\) bepaal je door een punt van de grafiek in te vullen:
\begin{align*}
\amp 5 = a \sqrt{-(-4-1)} \\
\Leftrightarrow \; \amp 5 = a \sqrt{5} \\
\Leftrightarrow \; \amp a = \sqrt{5}
\end{align*}
Voorbeeld 2.5.4. Transformaties van de grafiek van een elementaire functie.
Als er in de samenstelling meer dan twee functies voor de elementaire functie komen, moet je voorzichtig zijn bij het opsommen van de transformaties. Zo kan de functie \(f(x)=\sqrt{3x+6}\) geschreven worden als de samenstelling \(f= f_3 \circ f_2 \circ f_1 \) met
\begin{align*}
\amp f_1(x)=3x\\
\amp f_2(x)=x+6\\
\amp f_3(x)=\sqrt{x}
\end{align*}
Je mag hieruit echter niet besluiten dat je de grafiek van
\(f\) krijgt door de grafiek van
\(f_3\) te herschalen met een factor 1/3 volgens de
\(x\)-as, gevolgd door een verschuiving naar links met 6 eenheden! Om de juiste transformaties te bepalen, kan je de grafiek schetsen op basis van bovenstaande samenstelling (zie
Voorbeeld 2.5.1) of het functievoorschrift herschrijven als
\(f(x)=\sqrt{3}\cdot \sqrt{x+2}\text{.}\) \(f\) is dan te beschouwen als de samenstelling
\(f=f_5 \circ f_3 \circ f_4\) met
\begin{align*}
\amp f_4(x)=x+2\\
\amp f_3(x)=\sqrt{x}\\
\amp f_5(x)=\sqrt{3}x
\end{align*}
Belangrijk is dat de elementaire functie nu op de tweede plaats staat in de samenstelling! De transformaties die de grafiek van \(f_3\) transformeren in de grafiek van \(f\) zijn een verschuiving naar links met 2 eenheden, gevolgd door een herschaling met een factor \(\sqrt{3}\) volgens de \(y\)-as.
Het functievoorschrift herschrijven zodat er maar 1 functie voor de elementaire functie komt, is echter niet altijd mogelijk. Beschouw bijvoorbeeld de functie \(f(x)=\sqrt{-3x+6}\text{.}\) Je kan die beschouwen als de samenstelling \(f=f_3 \circ f_2 \circ f_1\) met
\begin{align*}
\amp f_1(x)=-3x\\
\amp f_2(x)=x+6\\
\amp f_3(x)=\sqrt{x}
\end{align*}
en na het schetsen van de grafiek (doe dit zelf!) kan je besluiten dat de grafiek van \(f_3\) in de grafiek van \(f\) wordt omgezet door een spiegeling om de \(y\)-as, een verschuiving naar rechts met 2 eenheden en een herschaling met factor \(\sqrt{3}\) volgens de \(y\)-as. Je kan het functievoorschrift ook herschrijven als \(f(x)=\sqrt{3} \cdot \sqrt{-(x-2)}\) en de tabel gebruiken die elke aanpassing van \(f(x)\) aan de corresponderende transformatie linkt:
\(\sqrt{x} \to \sqrt{-x}\text{:}\) spiegelen om de \(y\)-as;
\(\sqrt{-x} \to \sqrt{-(x-2)}\text{:}\) 2 eenheden naar rechts verschuiven.
\(\sqrt{-(x-2)} \to \sqrt{3} \cdot \sqrt{-(x-2)} \text{:}\) herschaling met een factor \(\sqrt{3}\) volgens de \(y\)-as;
Je kan hier niet steunen op een samenstelling om de transformaties te bepalen omdat er altijd minstens twee functies voor de elementaire functie komen. Bijvoorbeeld \(f=f_6 \circ f_3 \circ f_5 \circ f_4\) met
\begin{align*}
\amp f_4(x)=x-2\\
\amp f_5(x)=-x\\
\amp f_3(x)=\sqrt{x}\\
\amp f_6(x)=\sqrt{3}x
\end{align*}
Eerst naar rechts verschuiven met 2 eenheden en dan spiegelen om de \(x\)-as is niet de correcte volgorde!
Functievoorschrift bepalen op basis van de grafiek.
Lees de verschuivingen en spiegelingen af van de grafiek en stel de algemene vorm op van het functievoorschrift door het invoeren van een parameter die de herschaling volgens de \(y\)-as beschrijft.
Bepaal de waarde van de parameter door een punt van de grafiek in te vullen.