Naar de hoofdinhoud

Analyse: 3de graad ASO met 5 of 7 lesuren per week

Nele Vermeulen

Oefeningen 5.5 Oefeningen

De sinusfunctie

1.

Welke transformaties heb je nodig om van de grafiek van \(y=\sin x\) naar de grafiek van
  1. \(\displaystyle y=\sin (2x)-4\)
  2. \(\displaystyle y= 4 \sin (x) + \pi\)
  3. \(\displaystyle y= \sin \left [ 2 \left (x-\dfrac{\pi}{2} \right ) \right ]\)
  4. \(\displaystyle y=\sin(2x-10)\)
  5. \(\displaystyle y=\dfrac{1}{4} \sin \left [ 3 \left ( x-\pi \right ) \right ] -2\)
te gaan? Controleer jezelf met Desmos.
Oplossing.
a) herschalen volgens \(x\) met factor \(1/2\) en 4 eenheden naar beneden schuiven; b) herschalen volgens \(y\) met factor 4 en \(\pi\) eenheden naar boven schuiven; c) herschalen volgens \(x\) met factor \(1/2\) en \(\pi/2\) eenheden naar rechts schuiven; d) herschalen met factor \(1/2\) volgens \(x\) en 5 eenheden naar rechts schuiven; e) herschalen volgens \(x\) met factor \(1/3\text{,}\) \(\pi\) eenheden naar rechts schuiven, herschalen volgens \(y\) met factor \(1/4\) en 2 eenheden naar beneden schuiven.

2.

Om het functievoorschrift te bepalen als de grafiek gegeven is, ga je als volgt te werk:
  1. bepaal de evenwichtsstand \(d\) en de amplitude \(a\text{;}\)
  2. bepaal de periode \(T \Rightarrow b=\dfrac{2\pi}{T}\text{;}\)
  3. bepaal de horizontale verschuiving \(c\) door te kijken waar de sinusfunctie "begint" op de evenwichtslijn \(y=d\text{.}\)
Bepaal de functievoorschriften op slides 7 t.e.m 10 van de Desmosactiviteit over de sinusfunctie.
Oplossing.
11) \(4\sin\left(2x\right)+2\text{;}\) 12)\(3\sin\left(2x+\frac{\pi}{2}\right)\text{;}\) 13)\(2\sin\left(3x\right)-1\text{;}\) 14) \(4\sin\left(4x-\frac{\pi}{2}\right)+1\text{;}\) 15) \(2 \sin (1,2 \pi t) \)

3.

De uitwijking \(u\) van een slinger t.o.v. de verticale wordt bij benadering gegeven door \(u(t)= 6 \sin \pi t\) met \(t\) de tijd in seconden. Bepaal de periode en de amplitude van deze slingerbeweging.
Oplossing.
\(a=6\text{,}\) \(T=2\) s

4.

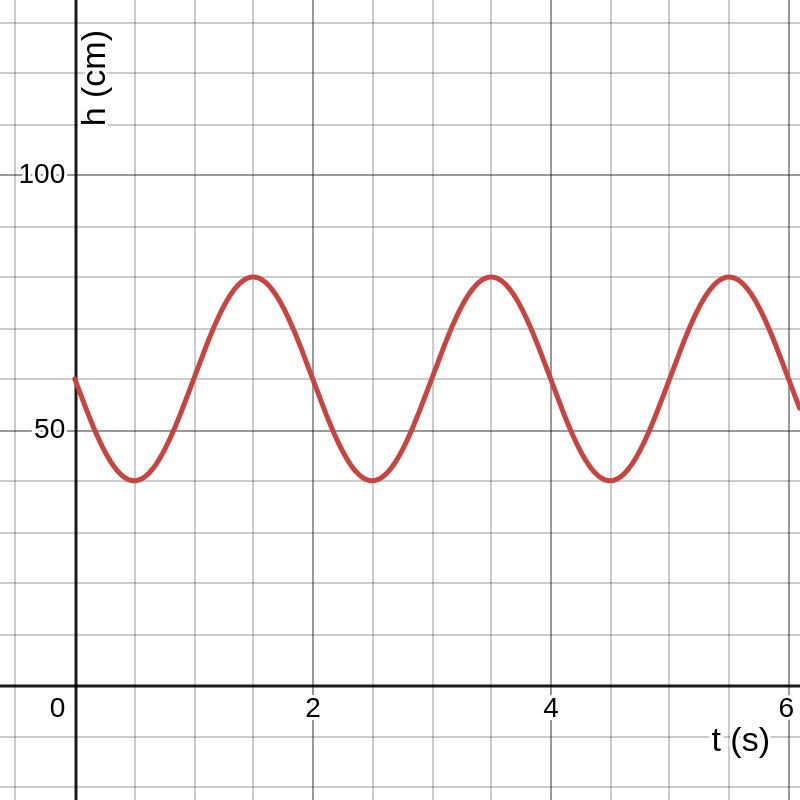
In een waterreservoir wordt de waterhoogte op een bepaalde dag beschreven door de functie
\begin{equation*} h=0,6 + \cos(0,4t) \end{equation*}
met \(t\) uitgedrukt in uren en \(h\) uitgedrukt in meter.
  1. Teken de grafiek van \(h\text{.}\)
  2. Welk deel van de grafiek is hier niet van toepassing?
  3. Geef de maximale waterhoogte.
  4. Wanneer is het reservoir voor de eerste keer droog?
  5. Kinderen mogen soms spelen in het reservoir als het water minder dan 40 cm hoog staat. Hoelang kunnen ze in de voormiddag vanaf 9 uur spelen?

5.

Een lieveheersbeestje zit op draaiende 33-toeren
 1 
Dit betekent 33 omwentelingen per minuut.
grammofoonplaat met een diameter van 35 cm. Op \(t=0\) bevindt het beestje zich op 12 cm rechts van het midden van de plaat. Stel dat \(x\) de afstand is in zijaanzicht van het beestje tot het midden van de plaat, dan geldt
\begin{equation*} x = 12 \sin 3,46(t-1,36) \end{equation*}
  1. Verklaar de getallen \(3,46\) en \(1,36\text{.}\)
  2. Schets de \(x(t)\)-grafiek.
  3. Wat verandert er aan de formule voor \(x(t)\) als het beestje naar het midden van de plaat kruipt?
  4. Wat verandert er aan de formule voor \(x(t)\) als het beestje in de draairichting van de plaat kruipt?

6.

Schrijf de functie \(f(x)=4 \sin (4x-2)+1\) als een samenstelling van 3 of meer functies en schets de grafiek.
Oplossing.
\(f=f_4 \circ f_3 \circ f_2 \circ f_1\) met \(f_1(x)=4x-2\text{,}\) \(f_2(x)=\sin x\text{,}\) \(f_3(x)=-4x\) en \(f_4(x)=x+1\)

7.

Voor de sinusfunctie is spiegelen van de grafiek om de \(x\)-as equivalent met een verschuiving naar links of rechts met \(\pi\) eenheden. Vertolk dit wiskundig en verklaar.

8.

Door gebruik te maken van de eigenschappen van verwante hoeken, kan het functievoorschrift van een samengestelde sinus- of cosinusfunctie steeds herschreven worden zodanig dat \(a\) en \(b\) positief zijn. Er geldt immers dat \(y=\sin(-x)=-\sin x=\sin (x+\pi)\text{.}\) Herschrijf de onderstaande functievoorschriften in de vorm \(f(x)=a \sin [b(x-c)]+d\) met \(a,b \gt 0\text{.}\)
  1. \(\displaystyle f(x)=-2 \sin(-x+4)\)
  2. \(\displaystyle f(x)= -3 \sin 4x\)
  3. \(\displaystyle f(x)=2 \sin (-3x)\)
Oplossing.
  1. \(\displaystyle -2\sin(-x+4)=2\sin(x-4)\)
  2. \(\displaystyle -3 \sin(4x)=3 \sin \left [4 \left (x+\frac{\pi}{4} \right )\right]\)
  3. \(\displaystyle 2\sin(-3x) = -2 \sin(3x)=2 \sin \left [3 \left (x+\frac{\pi}{3} \right )\right]\)

9.

Gegeven de functie \(f(x)=3 \sin \left (\dfrac{x}{2} - \dfrac{\pi}{12} \right )\) en de functie \(g\) bepaald door onderstaande grafiek. Stel het functievoorschrift \(g(x)\) op.

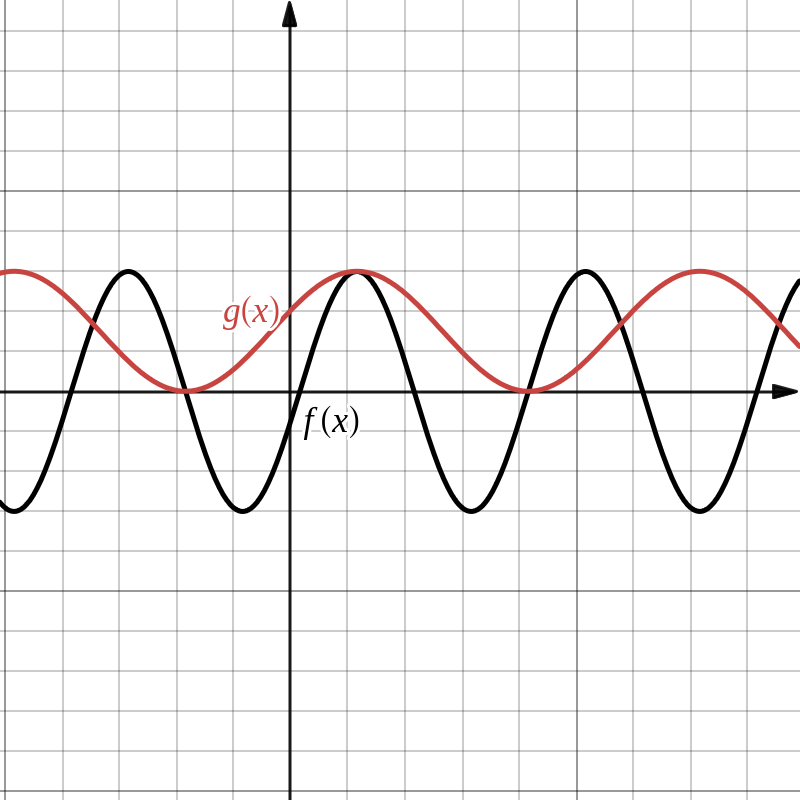
10.

De goniometrische functies zijn periodieke functies. Een functie \(f\) is periodiek als er een strikt positief getal \(T\) bestaat zodat
\begin{equation*} f(x+T)=f(x) \quad \forall x \in \text{dom} f \end{equation*}
\(T\) noemen we de periode van de functie.
Toon op basis van het functievoorschrift aan dat de periode van \(\cos bx\) gelijk is aan \(\frac{2\pi}{b}\text{.}\)

11.

(\(\star\))Door verschillende sinusfuncties op te tellen kan je allerlei periodieke functies maken. Onderstaande tekening toont bijvoorbeeld de grafiek van de functie \(f(x)=\sin(x)+\sin(3x)+\sin(5x)\)
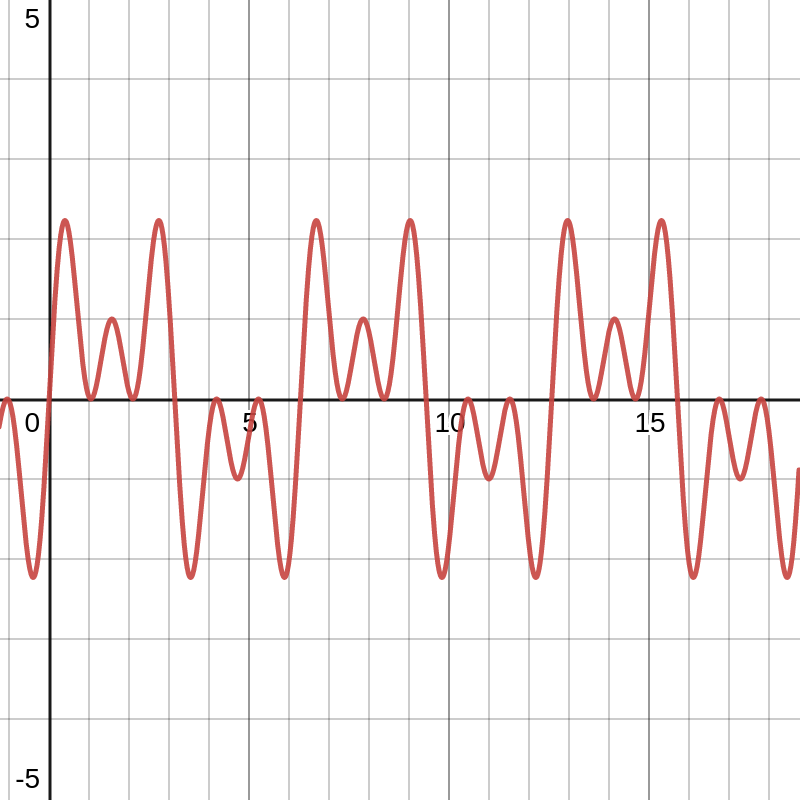
Als je twee sinusfuncties optelt waarvan de pulsaties weinig van elkaar verschillen, krijg je een erg typisch patroon. Hieronder zie je bijvoobeeld de grafiek die correspondeert met het optellen van twee zuivere tonen met frequenties van 440 Hz en 490 Hz. Hoe dit klinkt kan je hier
 2 
upload.wikimedia.org/wikipedia/commons/1/11/Schwebung.ogg
horen.
De functie is duidelijk periodiek, maar de amplitude zelf varieert ook periodiek. Om dit te begrijpen kunnen we één van de formules van Simpson (zie hieronder) toepassen: \(\sin p + \sin q = 2\sin \frac{p+q}{2} \cos \frac{p-q}{2} \text{.}\) De som van twee sinusfuncties is dus gelijk aan het product van een sinusfunctie en een cosinusfunctie of, anders geformuleerd, we krijgen een sinusfunctie waarvan de amplitude een cosinusfunctie is.
De formules van Simpson zijn:
\begin{align*} \amp 2\sin \alpha \cos \beta = \sin(\alpha+\beta)+\sin(\alpha-\beta) \amp \amp \sin p + \sin q = 2 \sin \frac{p+q}{2} \cos \frac{p-q}{2} \\ \amp 2\cos \alpha \sin \beta = \sin(\alpha+\beta)-\sin(\alpha-\beta) \amp \amp\sin p - \sin q = 2 \cos \frac{p+q}{2} \sin \frac{p-q}{2} \\ \amp 2\cos \alpha \cos \beta = \cos(\alpha+\beta)+\cos(\alpha-\beta) \amp \amp\cos p + \cos q = 2 \cos \frac{p+q}{2} \cos \frac{p-q}{2} \\ \amp -2\sin \alpha \sin \beta = \cos(\alpha-\beta)-\cos(\alpha+\beta) \amp \amp \cos p - \cos q = -2 \sin \frac{p+q}{2} \sin \frac{p-q}{2} \end{align*}
De formules van Simpson zijn in essentie gewoon combinaties van telkens twee som- of verschilformules. Beschouw bijvoorbeeld
\begin{align*} \amp \begin{cases} \sin(\alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \\ \sin(\alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \end{cases} \Bigg \rvert \begin{matrix} 1 \\ 1 \end{matrix} \Bigg \rvert \begin{matrix} 1 \\ -1 \end{matrix}\\ \Leftrightarrow \; \amp \begin{cases} \sin(\alpha + \beta ) + \sin(\alpha - \beta ) = 2 \sin \alpha \cos \beta \\ \sin(\alpha + \beta ) - \sin(\alpha - \beta ) = 2 \cos \alpha \sin \beta \end{cases} \end{align*}
Nu kunnen we de substituties
\begin{align*} \amp \begin{cases} \alpha + \beta = p \\ \alpha - \beta = q \end{cases} \Leftrightarrow \begin{cases} \alpha = \frac{p+q}{2} \\ \beta = \frac{p-q}{2} \end{cases} \end{align*}
doorvoeren:
\begin{equation*} \begin{cases} \sin p + \sin q = 2 \sin \frac{p+q}{2} \cos \frac{p-q}{2} \\ \sin p - \sin q = 2 \cos \frac{p+q}{2} \sin \frac{p-q}{2} \end{cases} \end{equation*}
Leid zelf de andere formules van Simpson af.

De cosinusfunctie

12.

Een reuzenrad draait rond met constante snelheid. De hoogte \(t\) seconden na het bereiken van het laagste punt wordt gegeven door \(h(t)=15-15 \cos (0,4t)\text{.}\)
  1. Schets de grafiek van \(h(t)\text{.}\)
  2. Na hoeveel seconden wordt de maximale hoogte bereikt?
  3. Wat is de maximale hoogte?
  4. Na hoeveel seconden is een bepaalde cabine op dezelfde plaats terug?
Oplossing.
Maximale hoogte van 30 m wordt bereikt na 7,85 s. Na 15,71 s is een cabine op dezelfde plaats terug.

13.

Schrijf \(f(x)=3 \cos (2x-6) -4\) als een algemene sinusfunctie.
Oplossing.
\(3 \cos (2x-6) -4 = 3 \sin \left [2 \left (x-3+\frac{\pi}{4} \right) \right ]-4\)

14.

Door welke transformaties ontstaat de grafiek van \(f(x)=2+\cos (x-2)\) uit de grafiek van \(\cos x\text{?}\) En door welke transformaties ontstaat de grafiek van \(f\) uit de grafiek van \(\sin x\text{?}\)
Oplossing.
\(\cos x\text{:}\) 2 eenheden naar rechts schuiven en 2 eenheden naar boven; \(\sin x\text{:}\) \(\frac{4-\pi}{2}\) eenheden naar rechts schuiven en 2 eenheden naar boven:
\begin{equation*} 2+\cos(x-2)=2+\sin \left(x-2+\frac{\pi}{2} \right)=2+\sin \left(x-\frac{4-\pi}{2} \right) \end{equation*}

15.

Phobos en Deimos zijn twee kleine maantjes van de planeet Mars. Ze bewegen in een cirkelbaan rond Mars, maar vanaf de aarde zien we ze ongeveer in een rechte horizontale lijn heen en weer bewegen. De afstand rechts van Mars noemen we positief en de afstand links van Mars negatief. De afstand van Phobos tot het middelpunt van Mars is 6500 km en Phobos draait in 7 uur rond Mars. Op \(t=0\) staat Phobos helemaal rechts van Mars.
  • Geef een formule voor de afstand van Phobos tot Mars.
  • De afstand van Deimos tot Mars is \(D(t)=24000 \cos(0,209(t-12))\) met \(D\) in km en \(t\) in uren. In hoeveel tijd draait Deimos om Mars?
  • Hoe ver staat Deimos van het middelpunt van Mars?
  • Wanneer zien we Deimos en Mars op dezelfde plaats?
  • Wanneer zien we Deimos en Phobos op dezelfde plaats (na \(t=0\)). Bepaal het antwoord grafisch m.b.v. Desmos.

Goniometrische functies afleiden

16.

Leid onderstaande functies af. Controleer jezelf met Geogebra.
  1. \(\displaystyle f(x)=2 \sin x + 3 \cos x\)
  2. \(\displaystyle f(x) = x \sin x\)
  3. \(\displaystyle f(x) = \sin x \cdot \cos 2x\)
  4. \(\displaystyle f(x) = \tan^2 x\)
  5. \(\displaystyle f(x) = x^3 \sin^2 x\)
  6. \(\displaystyle f(x)=\frac{2}{3} \sin^3 2x+ \sin 2x \cdot \cos^2 2x\)
  7. \(\displaystyle f(x) = \sin^2(3x+5)\)
  8. \(\displaystyle f(x) = \dfrac{1}{\cot x}\)
  9. \(\displaystyle f(x) = \cos \left (2x-1 \right )\)
  10. \(\displaystyle f(x) = \dfrac{\cos x}{2 \sin x - 3}\)
  11. \(\displaystyle f(x) = \dfrac{\sin x}{1+\tan^2 x}\)
  12. \(\displaystyle f(x) = \sin \left ((4x)^2 \right )\)
  13. \(\displaystyle f(x) = \sin \left (\frac{1}{x} \right ) \cos (-5x+2)\)

17.

Bepaal de raaklijn aan de grafiek van de functie \(f(x)=2x+ \dfrac{\sin x}{2}\) in het punt waarvoor \(x=\dfrac{\pi}{6}\text{.}\)

18.

Toon aan dat de tangensfunctie strikt stijgend is in elk interval \(\left ] -\dfrac{\pi}{2} +k\pi,\dfrac{\pi}{2}+k\pi \right [\) met \(k \in \mathbb{Z}\text{.}\)

19.

Onderstaande grafiek toont de hoogte in functie van de tijd voor een jongen die op een schommel zit.
  1. Stel het functievoorschrift \(h(t)\) op.
  2. Bepaal de gemiddelde verticale snelheid voor het interval \([0,2]\) s.
  3. Bepaal de ogenblikkelijke verticale snelheid op \(t=1\) s.
VorigTopVolgend