Sectie 5.4 Goniometrische functies afleiden
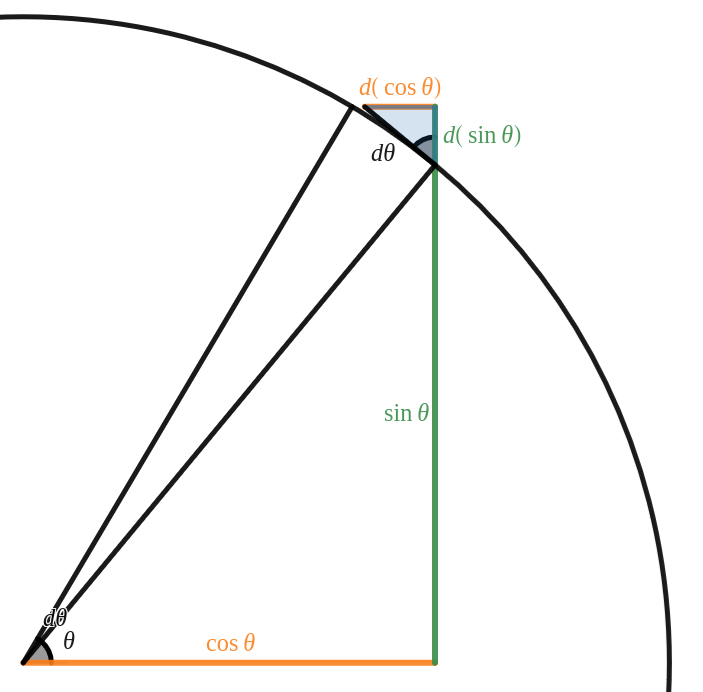
Voorbeeld 5.4.1. \(D(\sin \theta)\) en \(D(\cos \theta)\) bepalen via differentialen.
Een differentiaal \(df\) kan geïnterpreteerd worden als een oneindig kleine verandering. Door deze veranderingen te tekenen — weliswaar uitvergroot — kunnen sommige afgeleiden grafisch bepaald worden. Beschouw bijvoorbeeld onderstaande tekening van een deel van de goniometrische cirkel. Als de hoek \(\theta\) toeneemt met \(d\theta\) neemt de sinus toe met \(d(\sin \theta)\) en de cosinus af met \(d(\cos \theta)\text{.}\) Aangezien \(d\theta\) een oneindig kleine verandering is, is de schuine zijde van de kleine rechthoekige driehoek ook gelijk aan \(d\theta\) en geldt er dat
\begin{align*}
\amp D(\sin \theta) = \frac{d(\sin \theta)}{d\theta} = \cos \theta\\
\amp D (\cos \theta) = \frac{d(\cos \theta)}{d\theta} = - \sin \theta
\end{align*}
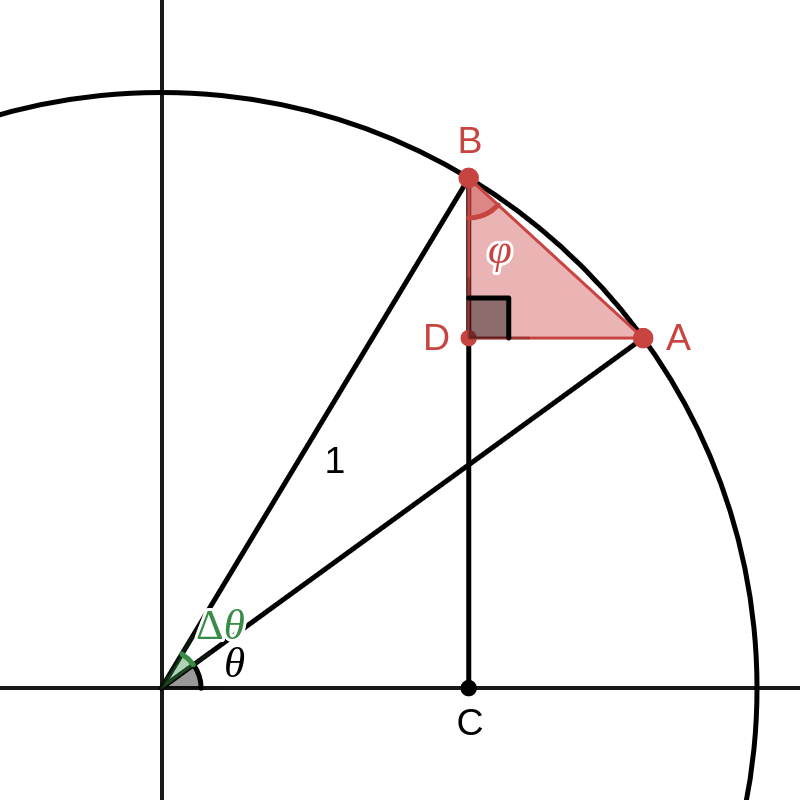
We bewijzen nu iets formeler dat \(D(\sin \theta)=\cos \theta\) en beperken ons daarbij opnieuw tot het eerste kwadrant.
\begin{align*}
D(\sin \theta) \amp = \lim_{\Delta \theta \to 0} \frac{\sin(\theta+\Delta \theta) - \sin \theta}{\Delta \theta}\\
\amp = \lim_{\Delta \theta \to 0}\frac{|BC|-|DC|}{\Delta \theta} \\
\amp = \lim_{\Delta \theta \to 0}\frac{|BD|}{\Delta \theta}
\end{align*}
In de rode rechthoekige driehoek geldt dat
\begin{equation*}
\cos \varphi = \frac{|BD|}{|BA|}
\end{equation*}
en we krijgen bijgevolg dat
\begin{equation*}
D(\sin \theta) = \lim_{\Delta \theta \to 0} \frac{ \cos \varphi |BA|}{\Delta \theta}
\end{equation*}
Als \(\Delta \theta \to 0\text{,}\) dan \(|BA| \to \Delta \theta\) (de straal is immers gelijk aan 1) en \(\varphi \to \theta\) (de rechte \(BA\) herleidt zich dan tot de raaklijn aan de cirkel in \(A\)) en bijgevolg is
\begin{equation*}
D(\sin \theta) =\cos \theta
\end{equation*}
Opdracht 5.4.1.
Vertrek van \(\cos x = \sin \left (x+\dfrac{\pi}{2}\right )\) om de formule voor \(D(\cos x)\) te bewijzen.
Goniometrische functies afleiden.
\begin{align*}
\amp D(\sin x) = \cos x \\
\amp D(\cos x) = - \sin x \\
\amp D(\tan x) = \frac{1}{\cos^2 x} \\
\amp D(\cot x) = - \frac{1}{\sin^2 x}
\end{align*}
Opdracht 5.4.2.
Aangezien \(\dfrac{f(x)}{g(x)}= f(x) \cdot \dfrac{1}{g(x)}\) kan je een quotiënt steeds afleiden via de productregel. Natuurlijk bestaat er ook een formule om een quotiënt rechtstreeks af te leiden:
\begin{equation*}
D\left(\dfrac{f(x)}{g(x)} \right)=\dfrac{Df(x)\cdot g(x)- f(x) \cdot Dg(x)}{\left[g(x) \right ]^2}
\end{equation*}
Bewijs deze formule.
Opdracht 5.4.3.
Bewijs de formules voor \(D(\tan x)\) en \(D(\cot x)\text{.}\)