Definitie 4.4.1. Differentiaal.
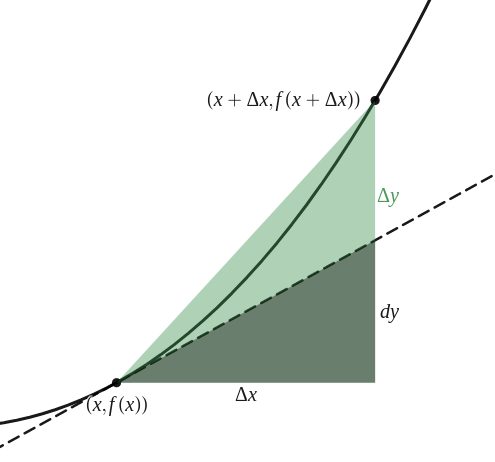
We definiëren de differentiaal van \(f\) als
\begin{equation*}
dy = df(x) = f'(x) \Delta x
\end{equation*}
Sectie 4.4 De differentiaal
De gemiddelde verandering van een functie \(f\) in het interval \([x,x+\Delta x]\) is een benadering is voor de puntsgewijze verandering \(f'(x)\) in \(x\text{.}\) Dit betekent dat we kunnen schrijven dat:
\begin{equation*}
\frac{\Delta y}{\Delta x} = f'(x) + \epsilon
\end{equation*}
met \(\epsilon\) het verschil tussen puntsgewijze en gemiddelde verandering. Hieruit leiden we af dat
\begin{equation*}
\Delta y = f'(x) \Delta x + \epsilon \Delta x
\end{equation*}
Dit betekent dat
\begin{equation*}
\Delta y = dy + \epsilon \Delta x
\end{equation*}
- \(\Delta y\) stelt de verandering in \(y\) voor langs de grafiek van \(f\) als \(x\) verandert met \(\Delta x\)
- \(dy\) stelt de verandering in \(y\) voor langs de raaklijn aan de grafiek van \(f\) als \(x\) verandert met \(\Delta x\)
Voor de functie \(f(x)=x\) geldt er dat \(\Delta x=dx\text{,}\) dus kunnen we stellen dat
\begin{equation*}
\boxed{dy = df(x) = f'(x) \; dx}
\end{equation*}
en dus dat
\begin{equation*}
f'(x)=\frac{dy}{dx}
\end{equation*}
Je kan een afgeleide dus beschouwen als een verhouding van differentialen en een differentiaal zelf als een oneindig kleine verandering. Merk op dat \(dy\) een functie is van zowel \(x\) als \(dx\) en we dus eigenlijk beter zouden schrijven dat \(dy=df(x,dx)\)
Opdracht 4.4.1.
Bereken
(a)
\(d(2x+1)\)
Antwoord.
\(d(2x+1) = 2 dx\)
(b)
\(d(x^2-3x)\)
Antwoord.
\(d(x^2-3x)=(2x-3)dx\)
Voorbeeld 4.4.2. Benaderingen berekenen met differentialen.
Een halfbolvormige koepel met diameter 8 meter dik wordt langs de buitenzijde belegd met bladgoud van 3 mm dik. Bereken bij benadering hoeveel goud hiervoor nodig is. (\(\rho_{\text{Au}}=19,3\) g/cm\(^3\)).
De straal verandert van 4 m naar 4,003 na aanbrengen van een goudlaag. Die verandering is niet oneindig klein, maar relatief gezien wel klein t.o.v. de straal zelf. We kunnen de verandering van het volume dus goed benaderen door de differentiaal \(dV\)
\begin{equation*}
dV = V'(r)\; dr = 2 \pi r^2 \; dr = 0,3016 \text{ m}^3
\end{equation*}
Hieruit volgt dat er ongeveer 5821 kg goud nodig is om de koepel te beleggen.
