Sectie 2.1 Basisbegrippen van functies
Om het concept van een functie beter te begrijpen kan je aan een machine denken. Niet zomaar gelijk welke machine, maar een machine met een invoer (input) en een uitvoer (output) zoals bijvoorbeeld
een fruitpers: je voert fruit in en je krijgt fruitsap terug. Wiskundig bekeken is dit niet zo’n interessante functie omdat je van fruitsap niet meer kan terugkeren naar het fruit dat je erin stopte. Een fruitpers is dus zoals de constante functie \(f(x)=c\) (\(c \in \mathbb{R}\)) die elke invoerwaarde \(x\) gewoon afbeeldt op \(c\text{.}\) We zeggen dat de functie \(f(x)=c\) niet inverteerbaar is. Op basis van de functiewaarde (de uitvoer) kan je niet meer achterhalen wat het argument (de invoer) was.
een lopende band die dekseltjes op doosjes met boter plaatst. Dit is een functie die wel inverteerbaar is: als je het deksel eraf haalt, heb je gewoon terug een doosje met boter.
Eigenlijk moet je een functie niet zozeer beschouwen als de machine zelf, maar eerder als het proces waarmee die machine een bepaalde invoerwaarde omzet naar een corresponderende uitvoerwaarde.
Nevenstaande tekening toont een functie die bollen omzet in kubussen. De verzameling van alle mogelijke objecten waarop het proces kan toegepast worden, noemen we het domein van die functie; de verzameling van alle mogelijke objecten die het resultaat zijn van het proces, noemen we het bereik. Een belangrijke beperking hierbij is wel dat een welbepaalde invoer (input) steeds een unieke uitvoer (output) heeft.
Als je een welbepaalde bol herhaaldelijk in de machine stopt, dan komt er ook steeds dezelfde kubus uitgerold. Stel bijvoorbeeld dat de machine het volume niet wijzigt en het domein gelijk is aan alle bollen met een straal kleiner dan of gelijk aan 5, dan is het bereik gelijk aan de verzameling van alle kubussen met een ribbe die kleiner dan of gelijk is aan \(5 \sqrt[3]{\frac{4}{3} \pi}\text{.}\)
Basisbegrippen van reële functies.
Een reële functie \(f\) koppelt aan elk reëel getal \(x\) hoogstens één reëel getal \(y\text{.}\)
-
We zeggen dat \(f\) aan het getal \(x\) de functiewaarde \(y\) toekent of dat \(y\) het beeld is van \(x\text{.}\) We noteren \(y=f(x)\) met \(f(x)\) het functievoorschrift van de functie \(f\text{.}\)
We noteren:
\begin{equation*}
\boxed{f: \mathbb{R} \to \mathbb{R}: x \to y=f(x)}
\end{equation*}
\(x\) is de invoerwaarde van de functie; vaak worden ook de termen argument of onafhankelijke variabele gebruikt. \(y\) is het beeld of de functiewaarde; vaak worden ook de termen uitvoerwaarde of afhankelijke variabele gebruikt.
Het domein (dom \(f\)) is de verzameling van alle \(x\)-waarden waarvoor \(f(x)\) bestaat. Je kan het domein grafisch bepalen door de grafiek van \(f\) te projecteren op de \(x\)-as.
Het bereik (ber \(f\)) is de verzameling van alle functiewaarden. Je kan het bereik grafisch bepalen door de grafiek van \(f\) te projecteren op de \(y\)-as.
De grafiek van \(f\) is de verzameling van alle punten \((x,y)\) waarvoor geldt dat \(y=f(x)\) en \(x \in \text{ dom } f\text{.}\)
Voorbeeld 2.1.2. Een watertank loopt vol.
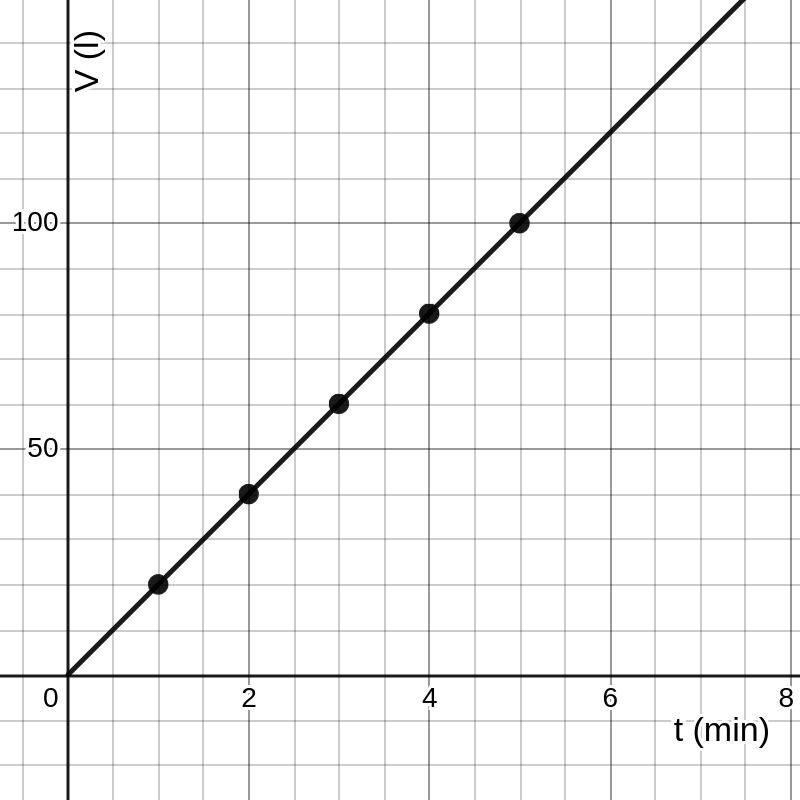
Beschouw een kegelvormige watertank met een straal van \(60\) cm en een hoogte van \(120\) cm. De tank wordt gevuld met water aan een snelheid van \(20\) l/min. Het volume \(V\) (in l) neemt dus rechtevenredig toe met de tijd \(t\) (in min). De reële functie \(f(t)\) die het verband beschrijft tussen het volume \(V\) en de tijd \(t\) kunnen we voorstellen met een functiewaardentabel, een grafiek of een functievoorschrift:
|
\(t\) (min) |
\(V\) (l) |
| 1 |
20 |
| 2 |
40 |
| 3 |
60 |
| 4 |
80 |
| 5 |
100 |
\(V=f(t)\) met \(f(t)=20t\)
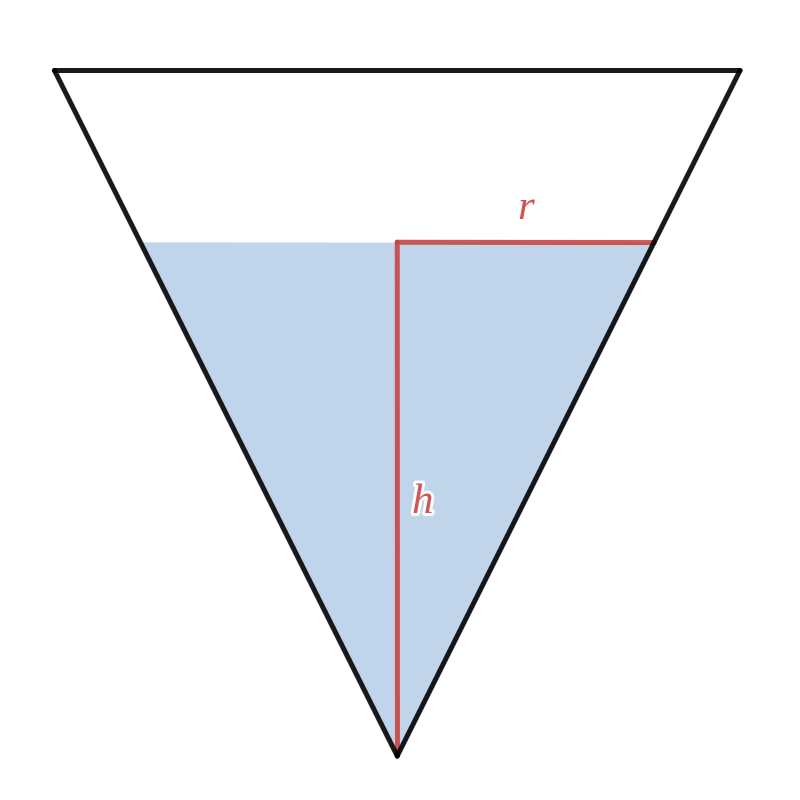
We willen nu bepalen hoe het waterniveau \(h\) verandert in functie van de tijd \(t\text{.}\) Hiervoor moeten we het functievoorschrift \(g(t)\) opstellen dat het verband tussen \(h\) en \(t\) beschrijft. Het volume water in de tank wordt gegeven door
\begin{equation*}
V= \frac{1}{3} \pi r^2 h
\end{equation*}
Voor deze specifieke tank geldt dat \(\dfrac{r}{h}=\dfrac{1}{2}\text{,}\) dus kunnen we schrijven dat
\begin{equation*}
V = \frac{\pi}{12} h^3
\end{equation*}
en hieruit volgt dat
\begin{equation*}
20 t = \frac{\pi}{12} h^3 \Leftrightarrow h = \sqrt[3]{\frac{240}{\pi}t}
\end{equation*}
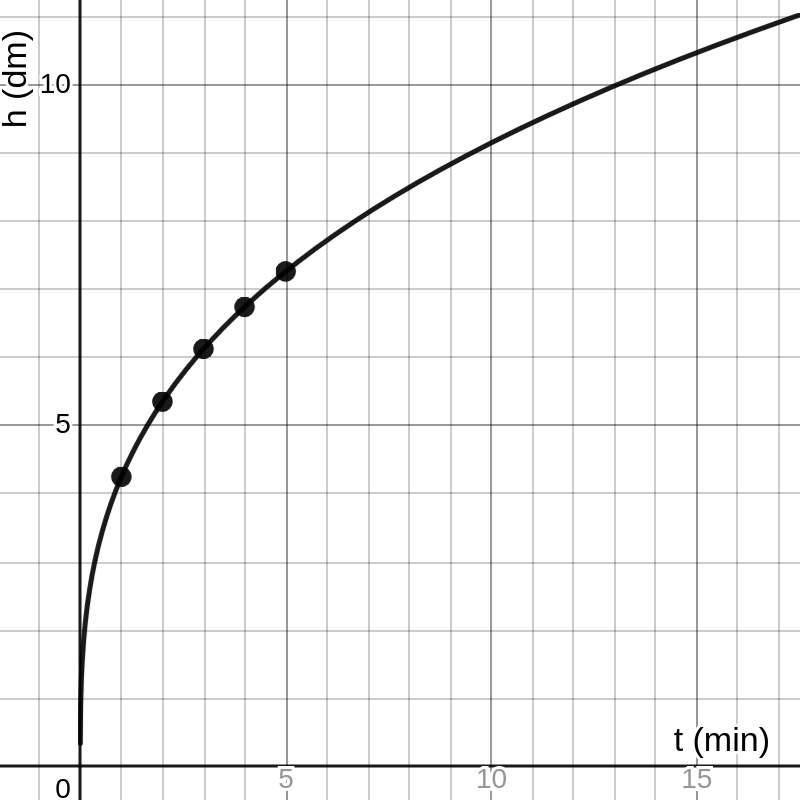
Op basis van dit functievoorschrift stellen we vervolgens een functiewaardentabel op en tekenen we de grafiek:
|
\(t\) (min) |
\(h\) (dm) |
| 1 |
4,2 |
| 2 |
5,3 |
| 3 |
6,1 |
| 4 |
6,7 |
| 5 |
7,3 |
De grafiek toont duidelijk dat de stijging van het waterniveau afneemt naarmate de tank meer gevuld is.
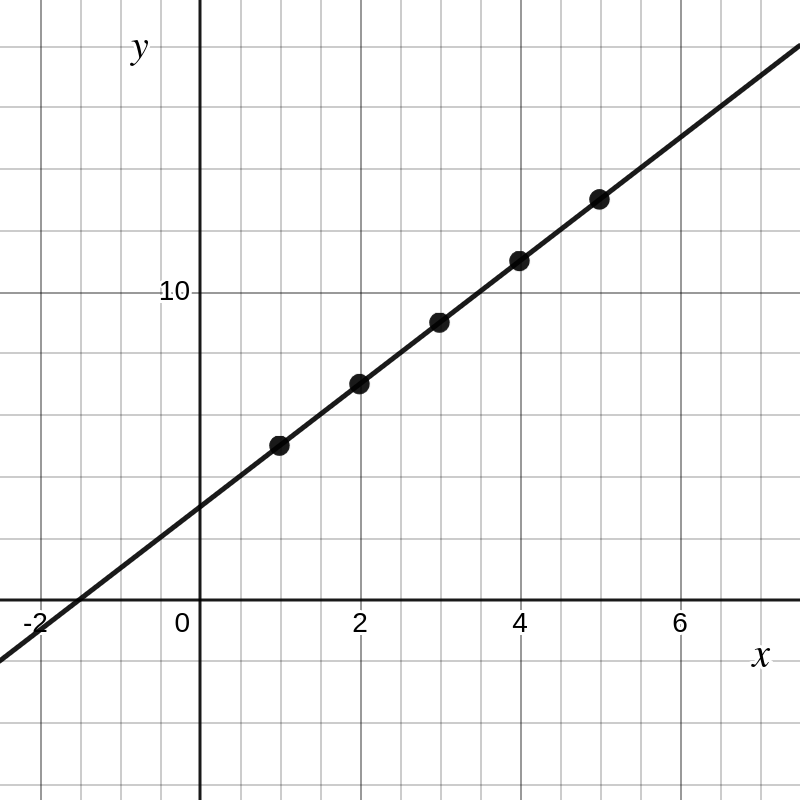
Voorbeeld 2.1.3. Een lineaire functie.
Gegeven een functie \(f\) die we achtereenvolgens toepassen op de getallen \(1, 2, 3, 4\) en \(5\text{.}\) De functiewaarden staan in onderstaande tabel:
| \(x\) |
\(f(x)\) |
| 1 |
5 |
| 2 |
7 |
| 3 |
9 |
| 4 |
11 |
| 5 |
13 |
Uit de tabel volgt onmiddelijk dat de functie \(f\) elke invoerwaarde vermenigvuldigt met 2 en bij dit resultaat vervolgens 3 optelt. Het functievoorschrift is dus \(f(x)=2x+3\text{.}\) De grafiek stelt een rechte voor en er geldt dat dom \(f = \mathbb{R}\) en ber \(f = \mathbb{R}\text{.}\)
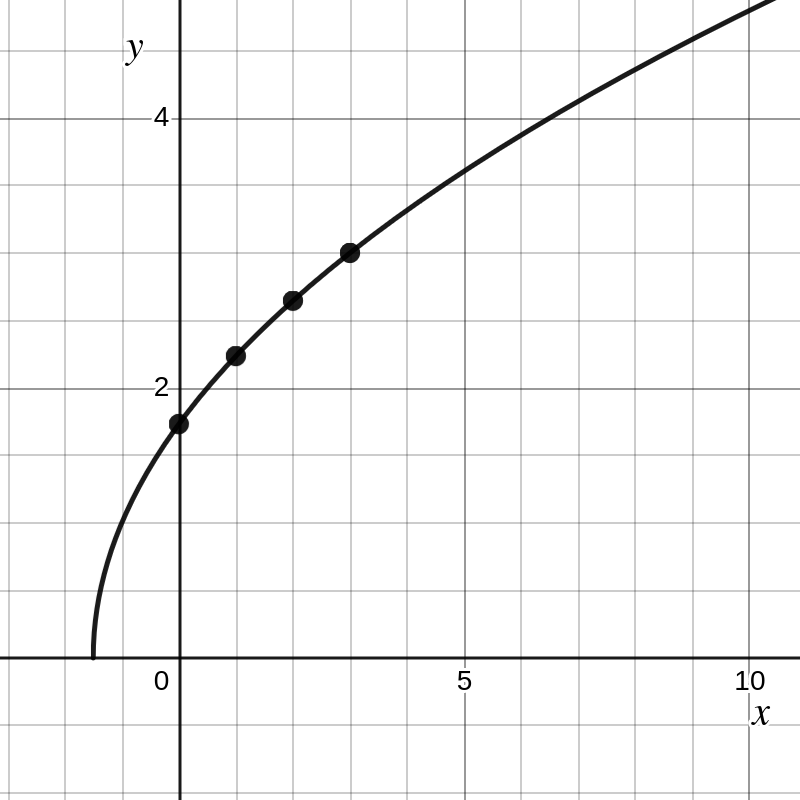
Voorbeeld 2.1.5. Een irrationale functie.
Gegeven de functie \(f\) met functievoorschrift \(f(x)=\sqrt{3x+2}\text{.}\) We berekenen enkele functiewaarden:
| \(x\) |
\(f(x)\) |
| 0 |
\(\sqrt{2}\) |
| 1 |
\(\sqrt{5}\) |
| 2 |
\(\sqrt{8}\) |
| 3 |
\(\sqrt{11}\) |
Aangezien de vierkantswortel van een negatief getal niet bestaat, vinden we het domein door te stellen dat \(3x+2 \ge 0 \Leftrightarrow x \ge -\frac{2}{3}\text{.}\) Er geldt dus dat dom \(f= \left [-\frac{2}{3},+\infty \right[\) en ber \(f=\mathbb{R}^+\text{.}\)
Voorbeeld 2.1.6. Wel of geen functie?
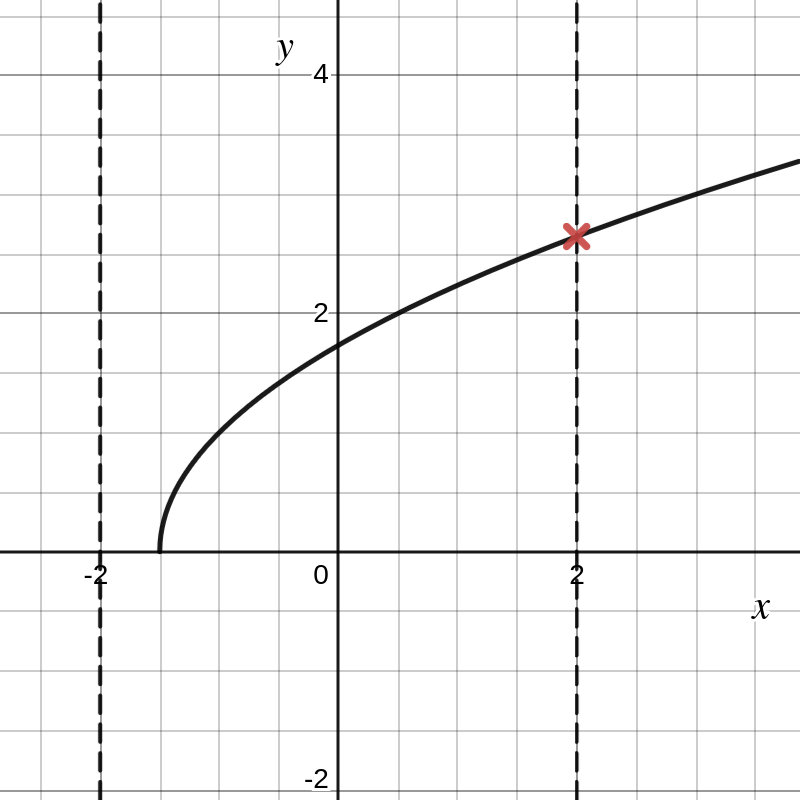
Het feit dat een reële functie aan elk argument \(x\) hoogstens één functiewaarde \(y\) koppelt, vertaalt zich grafisch in het volgende criterium:
Elke verticale lijn snijdt de grafiek van een functie hoogstens één keer.
Er doen zich hierbij slechts twee gevallen voor:
als \(x \in \mathrm{ dom } f\text{,}\) dan snijdt een verticale lijn door \((x,0)\) de grafiek in het punt \((x,f(x))\text{;}\)
als \(x \notin \mathrm{ dom } f\) dan snijdt een verticale lijn door \((x,0)\) de grafiek niet.
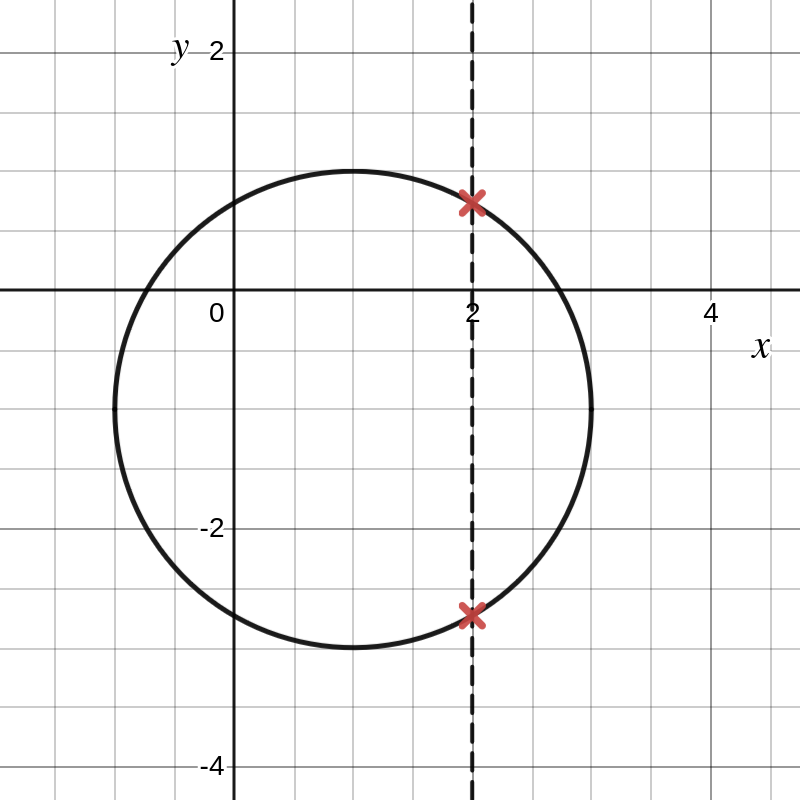
Een cirkel stelt niet de grafiek van een functie voor.
Voorbeeld 2.1.7. Het domein bepalen op basis van het functievoorschrift.
Om het domein van een functie te bepalen op basis van het functievoorschrift, hou je rekening met twee voorwaarden:
Beschouw bijvoorbeeld de functie \(f(x)=\dfrac{1}{x-2}\text{.}\) De noemer wordt nul als \(x=2\text{,}\) dus dom \(f=\mathbb{R} \setminus \lbrace 2 \rbrace\text{.}\) Een moeilijker voorbeeld: \(g(x)=\sqrt{|x-6|-1}\text{.}\) Het domein vinden we door te stellen dat \(|x-6|-1 \ge 0\text{.}\) Dit betekent \(|x-6| \ge 1\) en door toepassen van de definitie van absolute waarde, krijgen we
\begin{align*}
\amp x-6 \ge 1 \qquad \text{of} \qquad -x+6 \ge 1\\
\Leftrightarrow \; \amp x \ge 7 \qquad \text{of} \qquad x \le 5
\end{align*}
Dit betekent dat dom \(g = \mathbb{R} \; \setminus \; ] 5,7 [ \text{.}\)