Sectie 3.1 Het scalair product en de hoek tussen twee vectoren
Evenwijdige vectoren.
Twee vectoren \(\vv{u}(x_1,y_1)\) en \(\vv{v}(x_2,y_2)\) zijn evenwijdig als ze een veelvoud van elkaar zijn. Dit betekent dat hun coördinaten evenredig zijn:
\begin{equation*}
\vv{u} \parallel \vv{v} \Leftrightarrow \vv{u}=k \vv{v} \Leftrightarrow \frac{x_1}{x_2}=\frac{y_1}{y_2}=k
\end{equation*}
Om algebraïsch de hoek tussen twee vectoren te berekenen, kunnen we het scalair product of inproduct gebruiken.
Definitie 3.1.2.
Het scalair product of inproduct van twee vectoren \(\vv{u}\) en \(\vv{v}\) wordt gedefinieerd als
\begin{equation*}
\vv{u} \cdot \vv{v} = ||\vv{u}|| \cdot ||\vv{v}|| \cdot \cos \theta
\end{equation*}
met \(\theta\) de hoek tussen tussen de vectoren \(\vv{u}\) en \(\vv{v}\text{.}\)
Als één van de vectoren gelijk is aan de nulvector dan is het scalair product gelijk aan nul:
\begin{equation*}
\vv{u} \cdot \vv{o} = \vv{o} \cdot \vv{u} = 0
\end{equation*}
Merk op dat je deze formule op twee manieren kan interpreteren:
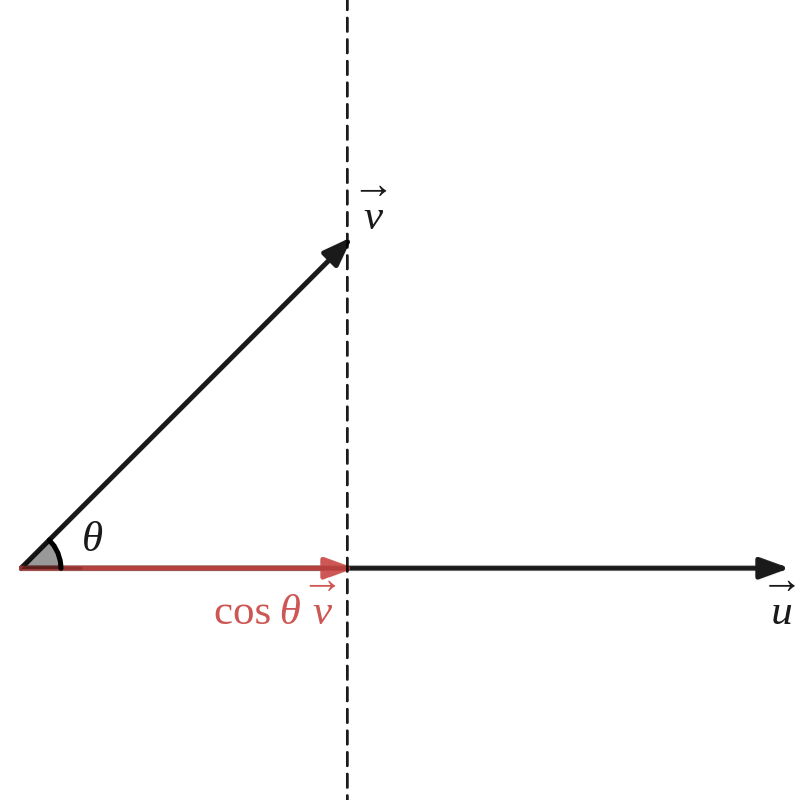
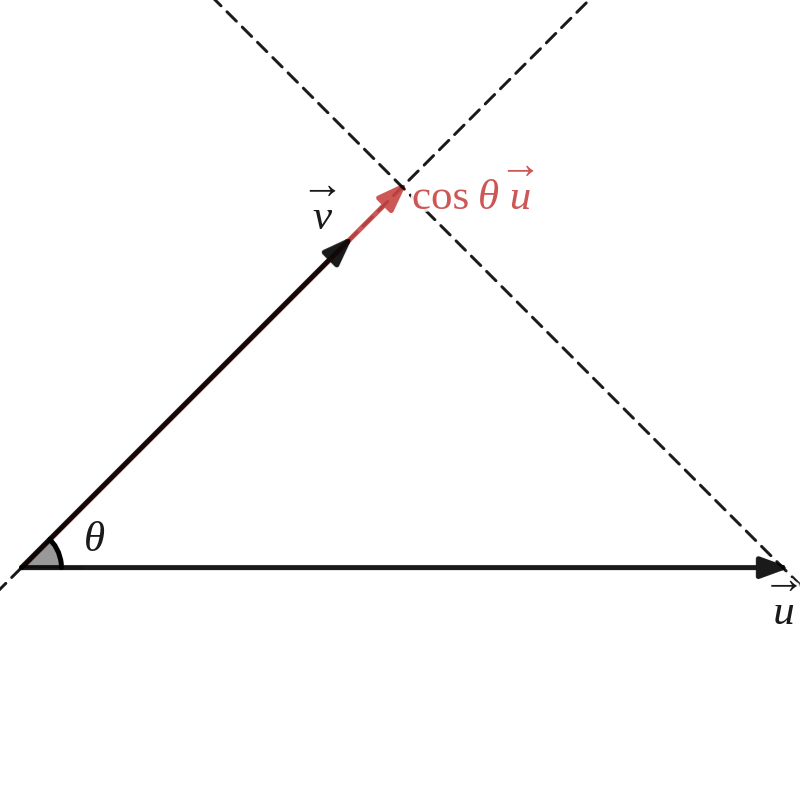
- Als het product van de norm van \(||\vv{u}||\) en de norm van de loodrechte projectie van \(\vv{v}\) op \(\vv{u}\text{.}\)
- Als het product van de norm van \(||\vv{v}||\) en de norm van de loodrechte projectie van \(\vv{u}\) op \(\vv{v}\text{.}\)
Loodrechte stand.
Twee vectoren \(\vv{u}\) en \(\vv{v}\text{,}\) verschillend van de nulvector, staan loodrecht op elkaar als en slechts als hun scalair product gelijk is aan nul.
\begin{equation*}
\vv{u} \cdot \vv{v} = 0 \Leftrightarrow \vv{u} \perp \vv{v}
\end{equation*}
Dit volgt onmiddellijk uit de definitie.
Eigenschappen van het scalair product.
- \(\displaystyle (\vv{u})^2=\vv{u} \cdot \vv{u} = ||\vv{u}||^2\)
- \(\displaystyle \vv{u} \cdot \vv{u} = 0 \Rightarrow \vv{u} = \vv{o}\)
- \(\displaystyle \vv{u} \cdot \vv{v} = \vv{v} \cdot \vv{u}\)
- \(\displaystyle \forall r \in \mathbb{R}: (r \vv{u}) \cdot \vv{v} = \vv{u} \cdot (r \vv{v}) = r (\vv{u} \cdot \vv{v})\)
- \(\vv{u} \cdot (\vv{v} + \vv{w}) = \vv{u} \cdot \vv{v} + \vv{u} \cdot \vv{w}\) en \((\vv{u} + \vv{v}) \cdot \vv{w} = \vv{u} \cdot \vv{w} + \vv{v} \cdot \vv{w}\)
Bovenstaande eigenschappen volgen onmiddellijk uit de definitie. Voor de laatste is dat wat moeilijker in te zien en kan een tekening verhelderend werken.
Opdracht 3.1.1.
Teken de laatste eigenschap van het scalair product. Kies één van beide.
Antwoord.
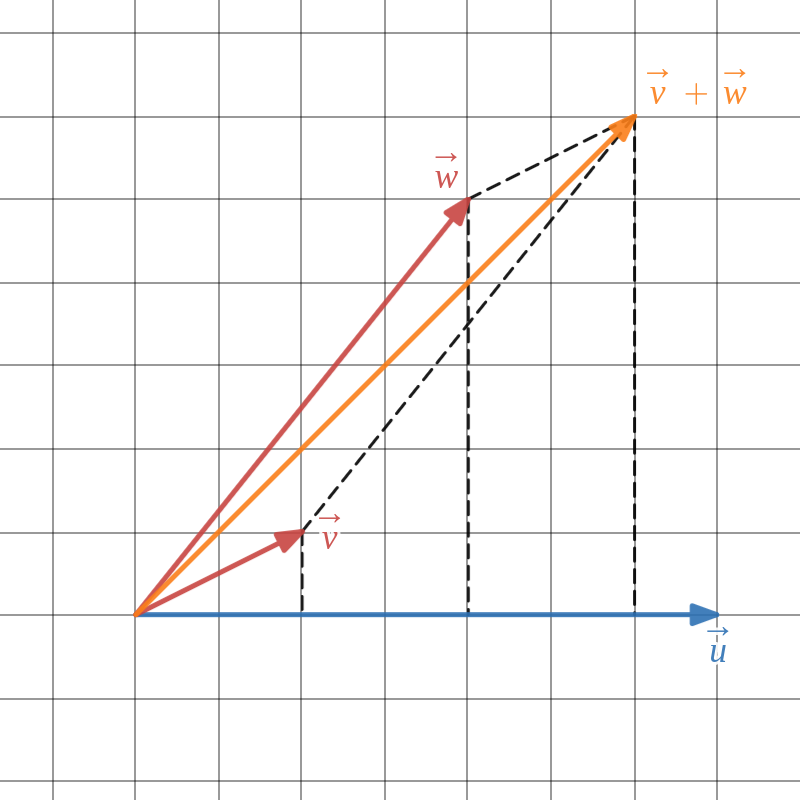
Uit bovenstaande tekening volgt:
\begin{align*}
\amp \vv{u} \cdot (\vv{v} + \vv{w}) = 7 \cdot 6 = 42 \\
\amp \vv{u} \cdot \vv{v} = 7 \cdot 2 = 14\\
\amp \vv{u} \cdot \vv{w} = 7 \cdot 4 = 28
\end{align*}
Het scalair product kan je ook berekenen op basis van de coördinaten van de twee vectoren. Gegeven de vectoren \(\vv{u}(x_1,y_1)\) en \(\vv{v}(x_2,y_2)\text{.}\) Het scalair product wordt
\begin{align*}
\vv{u} \cdot \vv{v} = \amp \vv{u} \cdot (x_2 \vv{E_x} + y_2 \vv{E_y})\\
= \amp x_2 (\vv{u} \cdot \vv{E_x}) + y_2 (\vv{u} \cdot \vv{E_y})\\
= \amp \boxed{x_2 x_1 + y_2 y_1}
\end{align*}
Door beide manieren van berekenen te combineren, kan de hoek \(\theta\) tussen de vectoren \(\vv{u}\) en \(\vv{v}\) bepaald worden:
\begin{align*}
\amp ||\vv{u}|| \cdot ||\vv{v}|| \cdot \cos \theta = x_1x_2+y_1y_2\\
\Rightarrow \; \amp \cos \theta = \frac{x_1 x_2 + y_1 y_2 + z_1 z_2}{||\vv{u}|| \; ||\vv{v}||}
\end{align*}
Hoek tussen twee vectoren.
De hoek \(\theta\) tussen de vectoren \(\vv{u}(x_1,y_1)\) en \(\vv{v}(x_2,y_2)\) kan berekend worden via
\begin{equation*}
\cos \theta = \frac{x_1 x_2 + y_1 y_2 }{||\vv{u}|| \; ||\vv{v}||}
\end{equation*}
Norm van een vector.
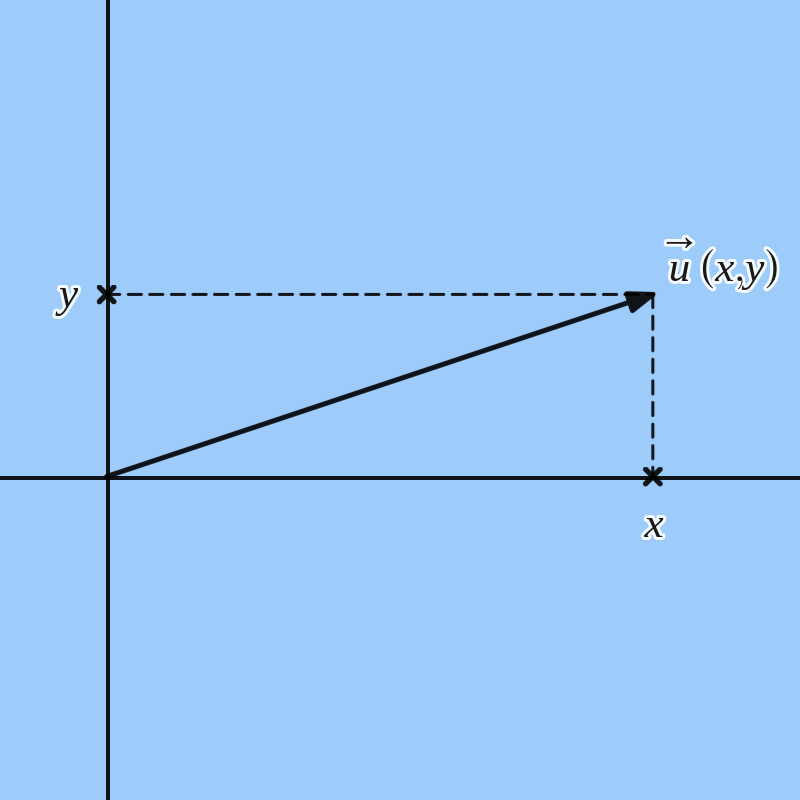
De norm van de vector \(\vv{u}(x,y)\) kan eenvoudig op basis van de coördinaten berekend worden:
\begin{equation*}
||\vv{u}|| = \sqrt{x^2+y^2}
\end{equation*}
Dit volgt gewoon uit de stelling van Pythagoras.
Opdracht 3.1.2.
Gegeven \(\vec{u}(x_1,y_1)\text{,}\) \(\vec{v}(x_2,y_2)\) en \(\vec{w}(x_3,y_3)\text{.}\) Bewijs dat \(\vv{u} \cdot (\vv{v} + \vv{w}) = \vv{u} \cdot \vv{v} + \vv{u} \cdot \vv{w}\text{.}\)
Opdracht 3.1.3.
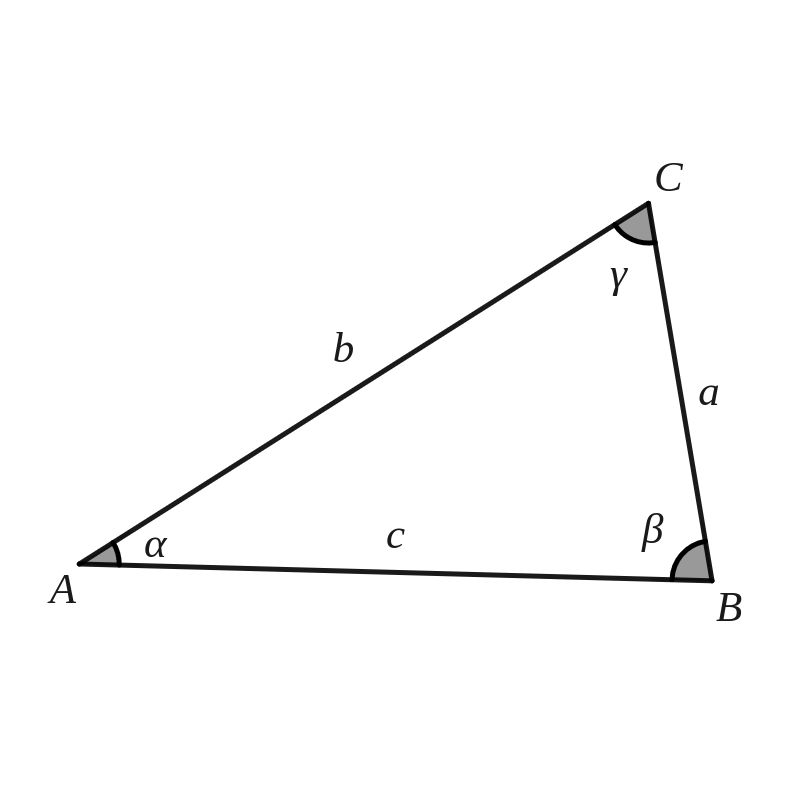
Bewijs de cosinusregel voor een willekeurige driehoek door \((\vv{AB})^2=(\vv{AC}+\vv{CB})^2\) uit te werken.