Naar de hoofdinhoud

Analytische vlakke meetkunde en kegelsneden: 3de graad ASO met 7 lesuren per week

Nele Vermeulen

Oefeningen 3.6 Oefeningen

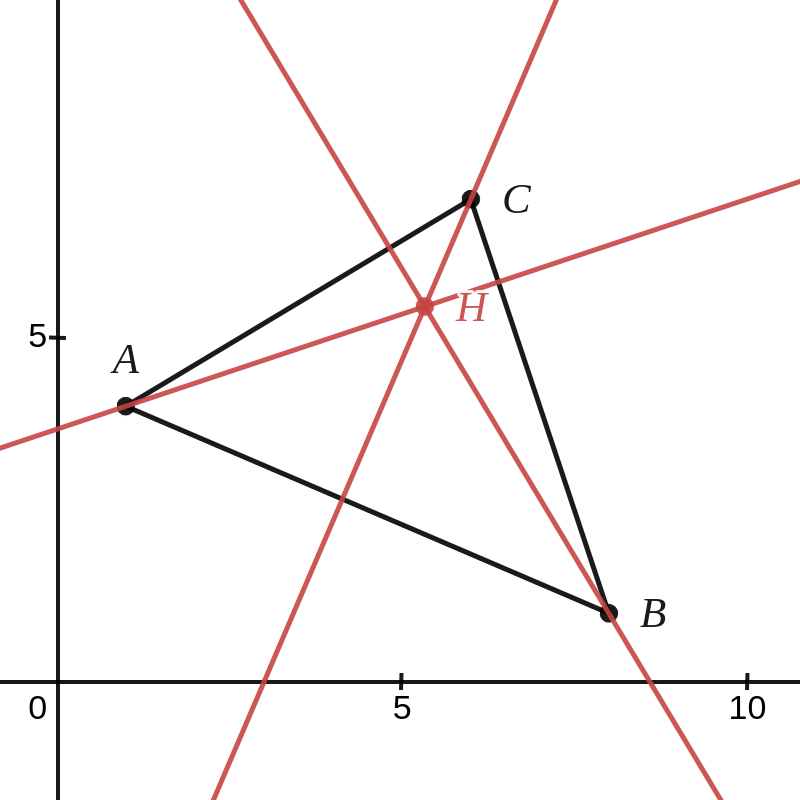
Het scalair product en de hoek tussen twee vectoren

1.

Gegeven \(A(3,-1)\text{,}\) \(B(4,3)\) en \(C(0,2)\text{.}\) Bereken:
  1. \(\displaystyle \vv{A} \cdot \vv{B}\)
  2. \(\displaystyle \vv{B} \cdot \vv{C}\)
  3. \(\displaystyle \vv{C} \cdot (\vv{A} - \vv{B})\)
  4. \(\displaystyle ||\vv{AB}||\)
  5. \(\displaystyle (\vv{A})^2\)
  6. \(\displaystyle ||\vv{A}+\vv{B}||\)
  7. de hoek tussen \(\vv{A}\) en \(\vv{B}\)
Antwoord.
Volg deze link
 1 
www.geogebra.org/geometry/hsdjpyev
.

2.

Beschouw de punten \(A(2,-1)\text{,}\) \(B(3,k)\text{,}\) \(C(-2,1)\) en \(D(0,3)\text{.}\)
  1. Voor welke \(k \in \mathbb{R}\) geldt dat \(AB \parallel CD\text{?}\)
  2. Voor welke \(k \in \mathbb{R}\) geldt dat \(AB \perp CD\text{?}\)
Oplossing.
\(\vv{AB}(1,k+1)\) en \(\vv{CD}(2,2)\text{,}\) dus evenwijdig als \(k=0\) en loodrecht als \(k=-2\text{.}\)

3.

Bepaal \(a\) zodat de hoek tussen \(\vv{u}(-3,a)\) en \(\vv{v}(1,2)\) gelijk is aan \(30\g\text{.}\)

4.

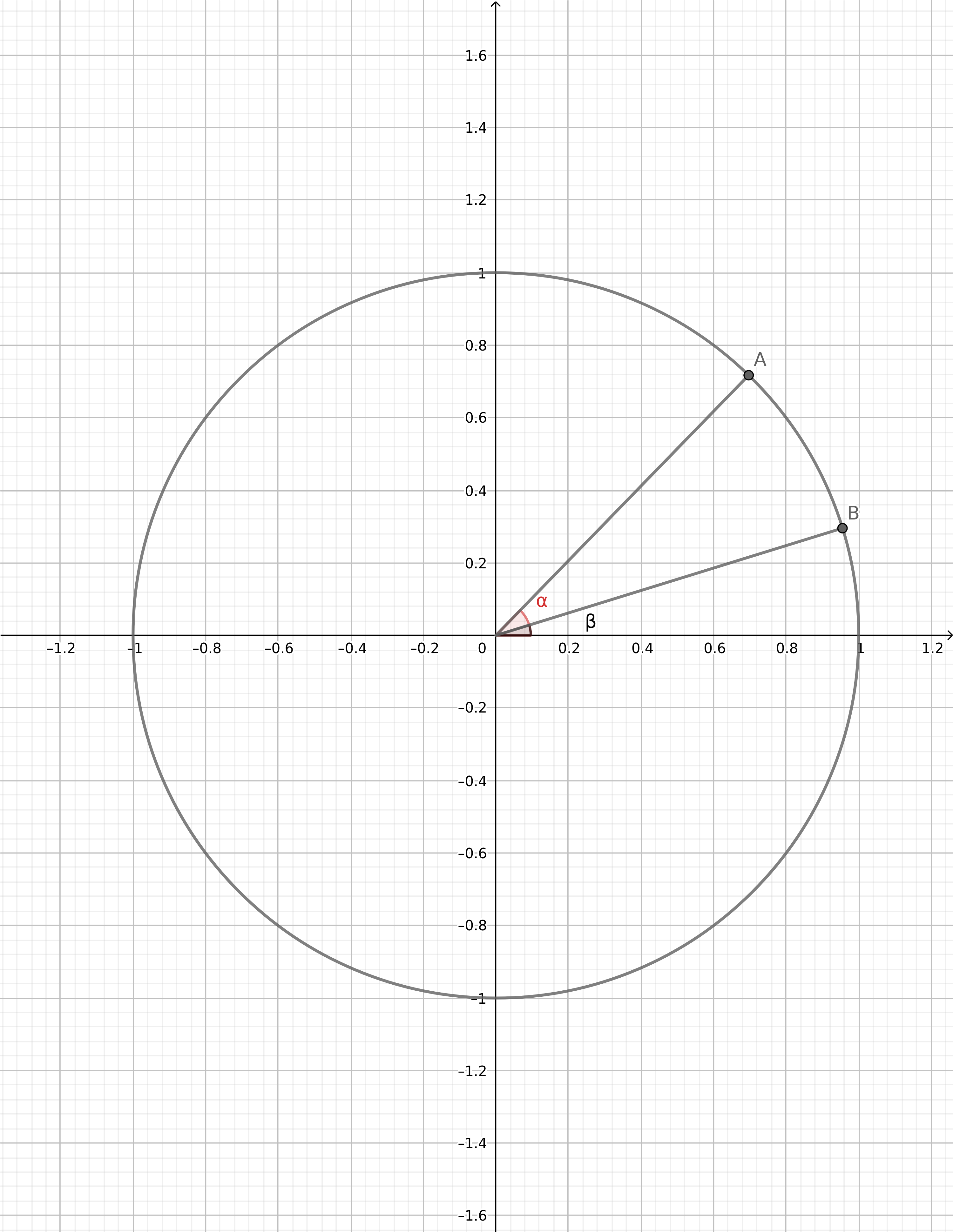
Gebruik het scalair product om te bewijzen dat \(\cos (\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta\text{.}\) Vertrek hierbij van de beeldpunten van de hoeken \(\alpha\) en \(\beta\) op de goniometrische cirkel.
Oplossing.
\(A(\cos \alpha, \sin \alpha)\) en \(B(\cos \beta, \sin \beta)\text{.}\) Er geldt dat \(\vv{A}\cdot \vv{B}=\cos (\alpha - \beta)\) (definitie scalair product), maar ook dat \(\vv{A} \cdot \vv{B} = \cos \alpha \cos \beta + \sin \alpha \sin \beta\) (via coördinaten).

5.

Bepaal de coördinaten van de loodrechte projectie van \(\vv{u}(-4,5)\) op \(\vv{v}(9,-2)\text{.}\)

6.

Gegeven onderstaande vierhoek met \(A(-2,3)\text{,}\) \(B(6,7)\) en punten \(P\) en \(Q\) die op de \(y\)-as liggen. Bepaal de coördinaten van \(P\) en \(Q\text{.}\)
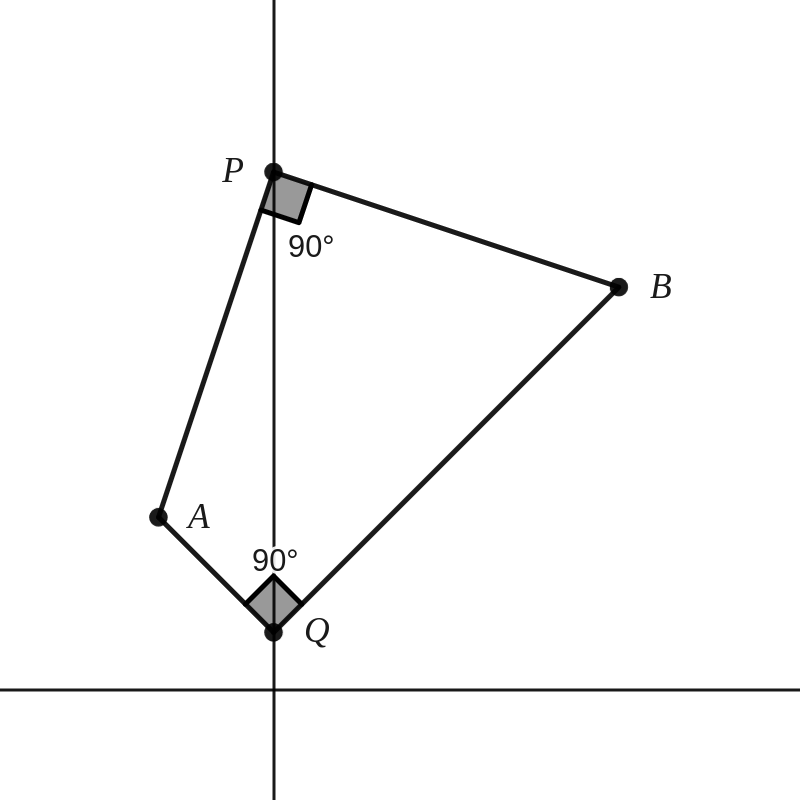
Antwoord.
\(Q(0,1)\) en \(P(0,9)\text{.}\)

Hoek tussen twee rechten

7.

Bepaal de hoek tussen onderstaande rechten. Controleer jezelf met Desmos of Geogebra.
  1. \(\begin{cases} x = 2-k \\ y= -3+5k \end{cases} \) en \(\begin{cases} x = 5-4k \\ y= 1 - 7 k \end{cases} \)
  2. \(\begin{cases} x = -3-4k \\ y= -3+3k \end{cases}\) en \(y=2x-5\)
  3. \(y=-5x-2\) en \(3x-5y=12\)

8.

De rechthoek \(ADEH\) bestaat uit drie congruente vierkanten en er geldt dat \(\vv{AB}(1,0)\) en \(\vv{AH}(0,1)\text{.}\) \(S\) is het snijpunt van de rechten \(AF\) en \(HD\text{.}\) Toon aan dat de rechten \(BS\) en \(HD\) loodrecht op elkaar staan.
Tip.
Bepaal eerst de coördinaten van het snijpunt \(S\text{:}\) \(S \left (\dfrac{6}{5},\dfrac{3}{5} \right )\text{.}\)

9.

Gegeven het punt \(P(5,2)\text{.}\) Bepaal de coördinaten van het punt \(Q\) op de rechte met vergelijking \(2x-3y+9=0\) zodat deze rechte een hoek van \(45\g\) maakt met de rechte \(PQ\text{.}\)
Tip.
Werk met een parametervoorstelling van de rechte \(2x-3y+9=0\text{.}\)
Antwoord.
\(Q(6,7)\)

De normaalvector en de cartesische vergelijking van een rechte

10.

De vorm \(ux+vy+w=0\) voor de cartesische vergelijking van een rechte is algemener dan de vorm \(y=ax+b\text{.}\) Leg uit!

11.

Gegeven de rechte met vergelijking \(5x-3y=7\text{.}\) Bepaal een normaalvector, richtingsvector en parametervoorstelling van deze rechte. Controleer jezelf m.b.v. Desmos.

12.

Gegeven drie punten \(P_1\text{,}\) \(P_2\) en \(P_3\text{.}\) Bepaal
  1. een richtingsvector van de rechte \(P_1P_2\text{;}\)
  2. een parametervoorstelling van de rechte \(P_1P_2\text{;}\)
  3. een normaalvector van de rechte \(P_1P_2\text{;}\)
  4. een cartesische vergelijking van de rechte \(P_1P_2\text{;}\)
  5. een cartesische vergelijking van de loodlijn uit \(P_3\) op de rechte \(P_1P_2\text{.}\)
  6. een cartesische vergelijking van de middelloodlijn van \([P_1P_2]\text{.}\)
Gebruik deze link: https://www.desmos.com/geometry/qqgtd3slyv om de drie punten te genereren en je rekenwerk te controleren.

13.

De cartesische vergelijking van een cirkel met straal \(4\) is gelijk aan \(x^2+y^2=16\text{.}\) De raaklijn in een punt aan een cirkel staat altijd loodrecht op de straal naar dit punt. Gebruik deze eigenschap om de raaklijn aan de cirkel in het punt \((2,2\sqrt{3})\) te bepalen. Controleer jezelf door een tekening te maken in Desmos.
Antwoord.
De vergelijking van de raaklijn is \(x+\sqrt{3}y-8=0\text{.}\)

14.

Bepaal de loodrechte projectie \(P'\) van het punt \(P(3,2)\) op de rechte \(y=\dfrac{3}{2}x\text{.}\)
Tip.
Je zoekt het snijpunt van de rechte en de loodlijn uit \(P\) op de rechte.
Antwoord.
\(P'\left ( \dfrac{24}{13},\dfrac{36}{13}\right)\)

15.

Gegeven de driehoek \(ABC\) met \(A(1,4)\text{,}\) \(B(8,1)\) en \(C(6,7)\text{.}\) Stel parametervoorstellingen op van alle hoogtelijnen en bepaal de coördinaten van het snijpunt \(H\text{.}\)
Antwoord.
hoogtelijn uit \(C\text{:}\) \(\begin{cases} x = 6 + 3k \\ y = 7 + 7k \end{cases}\text{;}\) hoogtelijn uit \(B\text{:}\) \(\begin{cases} x = 8 - 3k \\ y = 1 + 5k \end{cases}\text{;}\) hoogtelijn uit \(A\text{:}\) \(\begin{cases} x = 1 - 6k \\ y = 4 - 2k \end{cases}\text{;}\) \(H \left (\dfrac{16}{3} , \dfrac{49}{9} \right )\)

Afstanden in het vlak

16.

Gegeven de rechte met vergelijking \(y=2x+3\) en het punt \(P(11,5)\text{.}\) Welke punten van de rechte liggen op een afstand \(10\) van \(P\text{?}\)
Antwoord.
\((5,13)\) en \((1,5)\)

17.

Gegeven de twee evenwijdige rechten \(3x+4y=-10\) en \(6x+8y=30\text{.}\) Bepaal de afstand tussen deze twee rechten.
Antwoord.
\(5\)

Meetkundige plaatsen in het vlak

18.

Bepaal de verzameling punten \(P\) van het vlak die op een afstand 3 van het punt \((-1,2)\) liggen.

19.

Gegeven de rechten \(a \leftrightarrow 2x-y+1=0\) en \(b \leftrightarrow x-2y+8=0\text{.}\) Bepaal de verzameling punten \(P\) van het vlak die even ver verwijderd zijn van \(a\) en \(b\text{.}\)

20.

Gegeven de rechten \(a \leftrightarrow y=2x-3\) en \(b \leftrightarrow 2y-4x-5=0\text{.}\) Bepaal de verzameling punten \(P\) van het vlak die even ver verwijderd zijn van \(a\) en \(b\text{.}\)
VorigTopVolgend