Sectie 4.2 Cartesische vergelijking van een parabool
Een parabool is de verzameling punten van het vlak waarvoor de afstand tot een gegeven punt — het brandpunt — gelijk is aan de afstand tot een gegeven rechte — de richtlijn.
Opdracht 4.2.1.
We gaan nu op basis van bovenstaande definitie de cartesische vergelijking van een parabool afleiden.
Kies een orthonormaal assenstelsel waarbij de \(x\)-as de loodlijn uit het brandpunt \(F\) op de richtlijn \(r\) is. De \(x\)-as is bovendien zo georiënteerd dat het brandpunt rechts van de richtlijn ligt. Noem \(E\) het snijpunt van de \(x\)-as met de richtlijn. De \(y\)-as is dan de middelloodlijn van \([EF]\text{.}\) Teken brandpunt, richtlijn en dit assenstelsel.
Stel nu dat \(d(F,r)= d(F,E) = p\) en leidt hieruit de coördinaten van \(F\) en de cartesische vergelijking van de richtlijn af.
Voor een willekeurig punt \(P(x,y)\) van de parabool moet gelden dat \(d(P,F)=d(P,r)\text{.}\) Stel deze gelijkheid op en werk uit tot je de vergelijking \(y^2=2px\) krijgt.
Voeg een schets van een parabool aan je tekening toe. Kies zelf een waarde voor \(p\text{.}\)
Topvergelijking van een parabool.
De topvergelijking van een parabool is
\begin{equation*}
y^2=2px
\end{equation*}
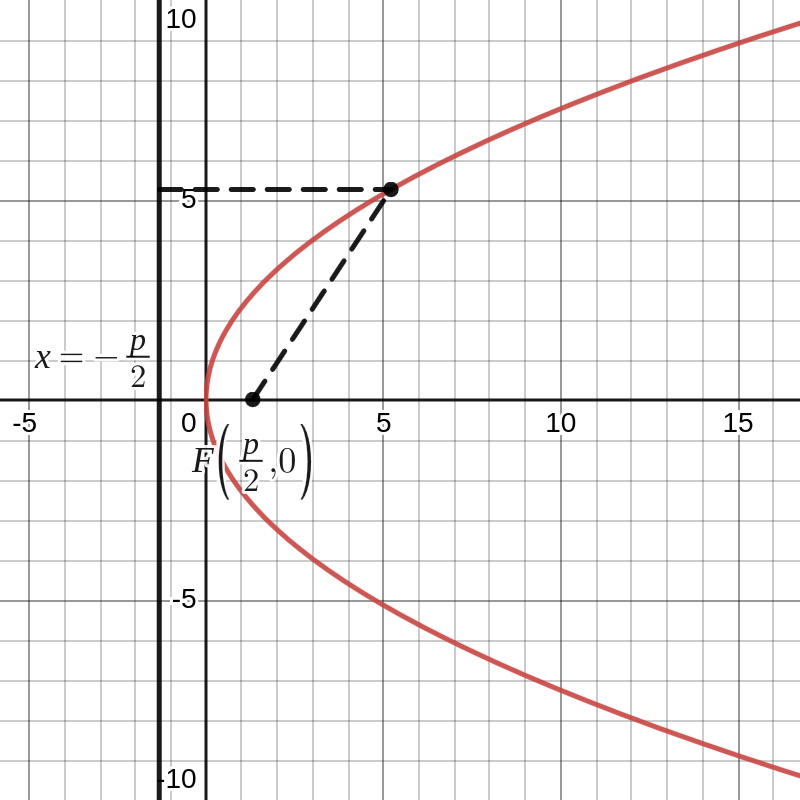
met \(p \in \mathbb{R}^+_0\text{.}\) De parameter \(p\) bepaalt de opening van de parabool. Er geldt
de top is \(O(0,0)\text{;}\)
het brandpunt is \(F\left ( \dfrac{p}{2},0 \right )\text{;}\)
de vergelijking van de symmetrie-as is \(y=0\)
de vergelijking van de richtlijn is \(x=-\dfrac{p}{2}\)
Bovenstaande vergelijking is de standaardvorm van de topvergelijking. We bespreken kort enkele alternatieve mogelijkheden. (
Link naar Desmos tekening)
-
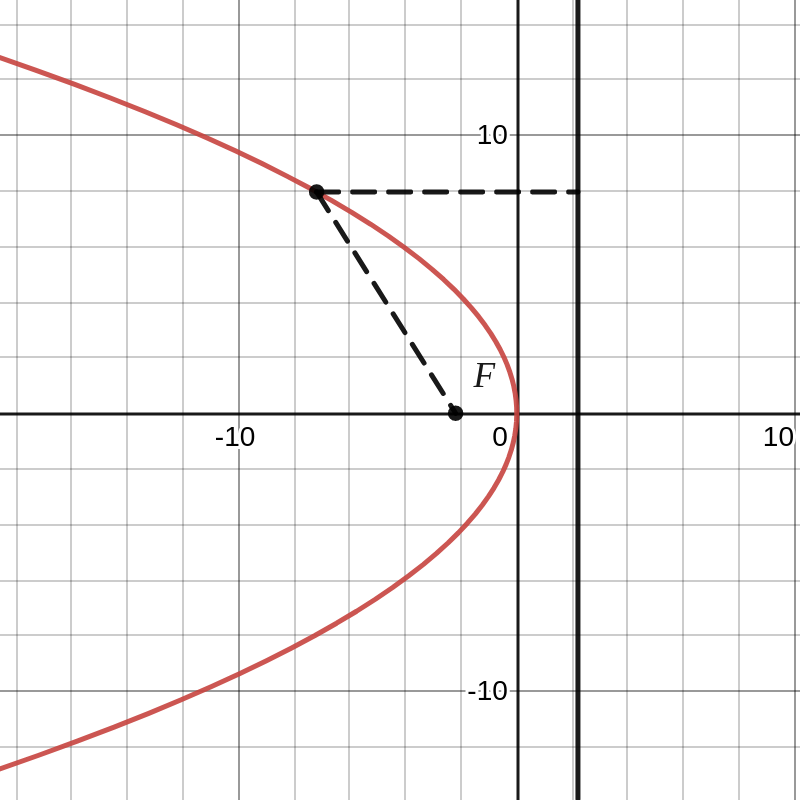
Als we de positie van het brandpunt en de richtlijn omwisselen, krijgen we de parabool met vergelijking
\begin{equation*}
\boxed{y^2=-2px}
\end{equation*}
Er geldt nu
de top is \(O(0,0)\text{;}\)
het brandpunt is \(F\left (-\dfrac{p}{2},0 \right )\text{;}\)
de vergelijking van de symmetrie-as is \(x=0\)
de vergelijking van de richtlijn is \(x=\dfrac{p}{2}\)
-
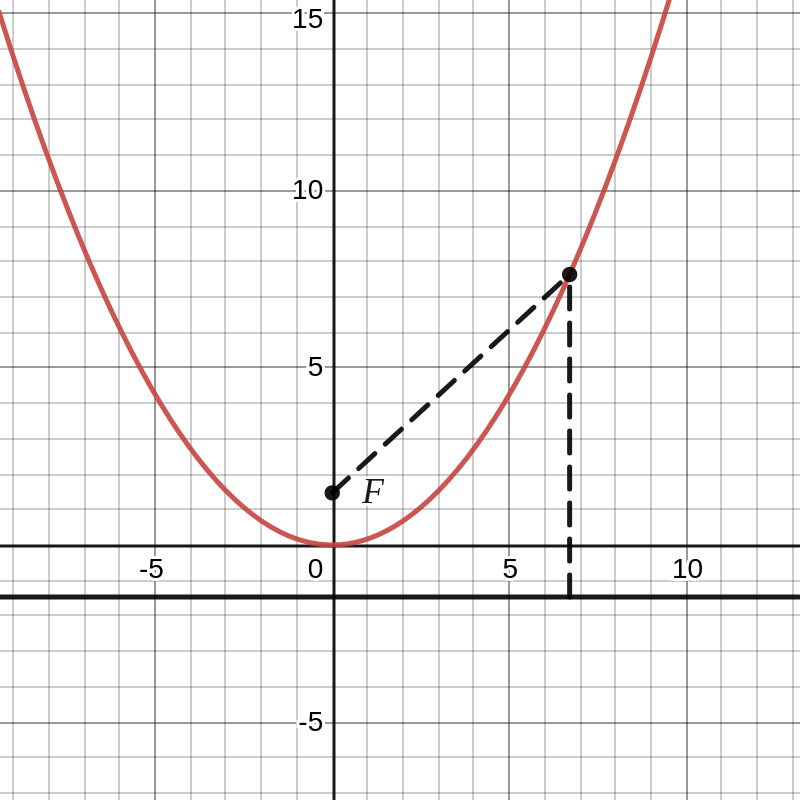
Als we de parabool \(y^2=2px\) spiegelen t.o.v. \(y=x\text{,}\) krijgen we de parabool
\begin{equation*}
\boxed{x^2 = 2py} \Leftrightarrow y=\frac{1}{2p}x^2
\end{equation*}
die de grafiek van een kwadratische functie is. Er geldt nu
de top is \(O(0,0)\text{;}\)
het brandpunt is \(F\left (0, \dfrac{p}{2} \right )\text{;}\)
de vergelijking van de symmetrie-as is \(x=0\)
de vergelijking van de richtlijn is \(y=-\dfrac{p}{2}\)
-
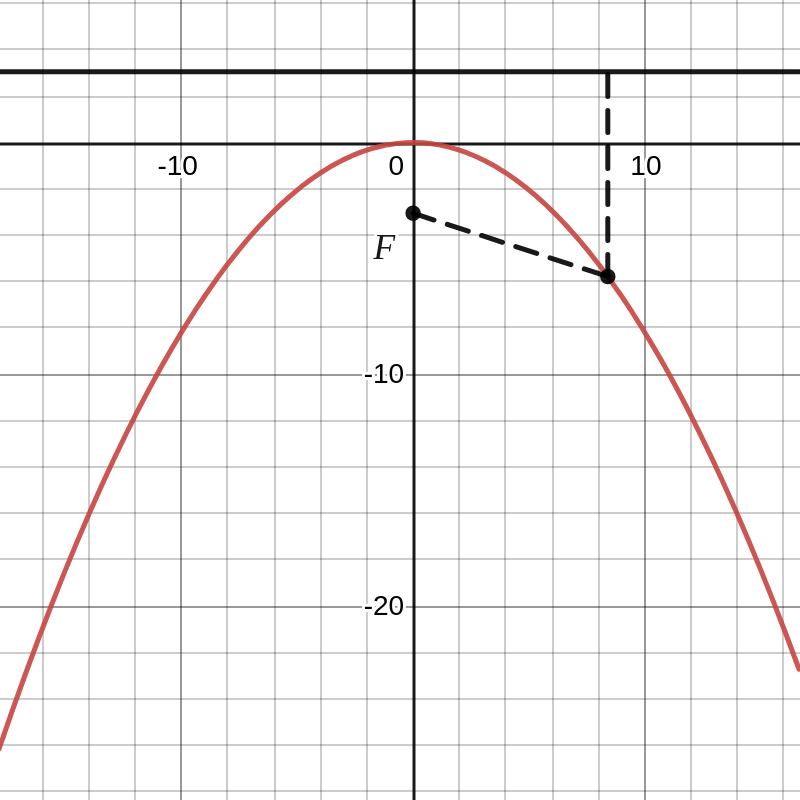
Bij deze gespiegelde versie, wisselen we nu opnieuw de positie van brandpunt en richtlijn. Dit geeft
\begin{equation*}
\boxed{x^2 = -2py}
\end{equation*}
Er geldt nu
de top is \(O(0,0)\text{;}\)
het brandpunt is \(F\left (0, -\dfrac{p}{2} \right )\text{;}\)
de vergelijking van de symmetrie-as is \(x=0\)
de vergelijking van de richtlijn is \(y=\dfrac{p}{2}\)