Sectie 1.4 Vectoren ontbinden
Stel dat we onderstaande vraag willen beantwoorden.
Een blok staat op een hellend vlak dat een hoek van \(20^{\circ}\) maakt met de horizontale. De zwaartekracht uitgeoefend op het blok bedraagt 100 N. Gaat het blok schuiven als de maximale wrijvingskracht gelijk is aan 38 N?
Om deze vraag te beantwoorden, moeten we de zwaartekracht \(\vv{F}_z\) ontbinden in twee componenten \(\vv{F}_{z\perp}\) en \(\vv{F}_{z\parallel}\) met \(\vv{F}_{z\perp}\) loodrecht op de helling en \(\vv{F}_{z\parallel}\) evenwijdig met de helling. \(\vv{F}_z\) ontbinden in twee componenten betekent gewoon \(\vv{F}_z\) schrijven als de som van twee vectoren:
\begin{equation*}
\vv{F}_z=\vv{F}_{z\perp}+\vv{F}_{z\parallel}
\end{equation*}
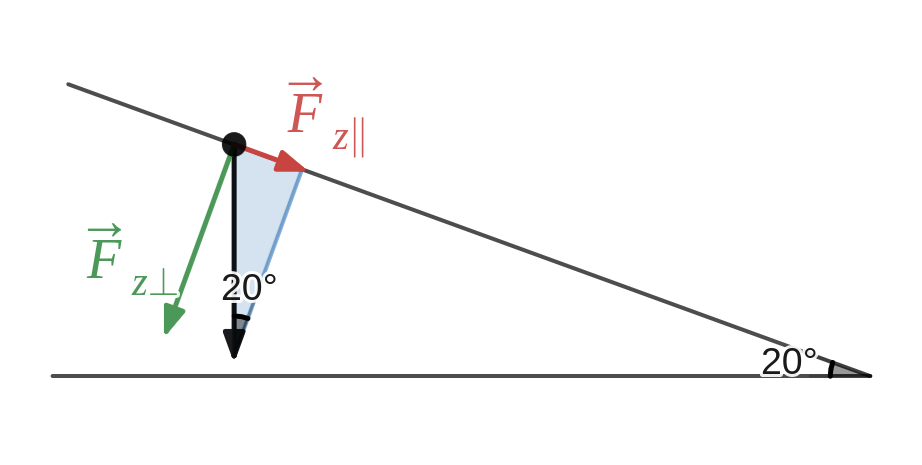
Als \(\vv{F}_{z\parallel}\) groter is dan 38 N, dan zal het blok naar beneden glijden. In de aangeduide rechthoekige driehoek geldt \(\sin 20^{\circ}=\dfrac{||\vv{F_{z \parallel}}||}{||\vv{F_z}||}\) en hieruit volgt dat \(||\vv{F_{z \parallel}}||= ||\vv{F_z}|| \sin 20^{\circ} = 34,2\) N. Het blok blijft dus staan op de helling.
