Sectie 3.4 Afstanden in het vlak
Afstand tussen twee punten.
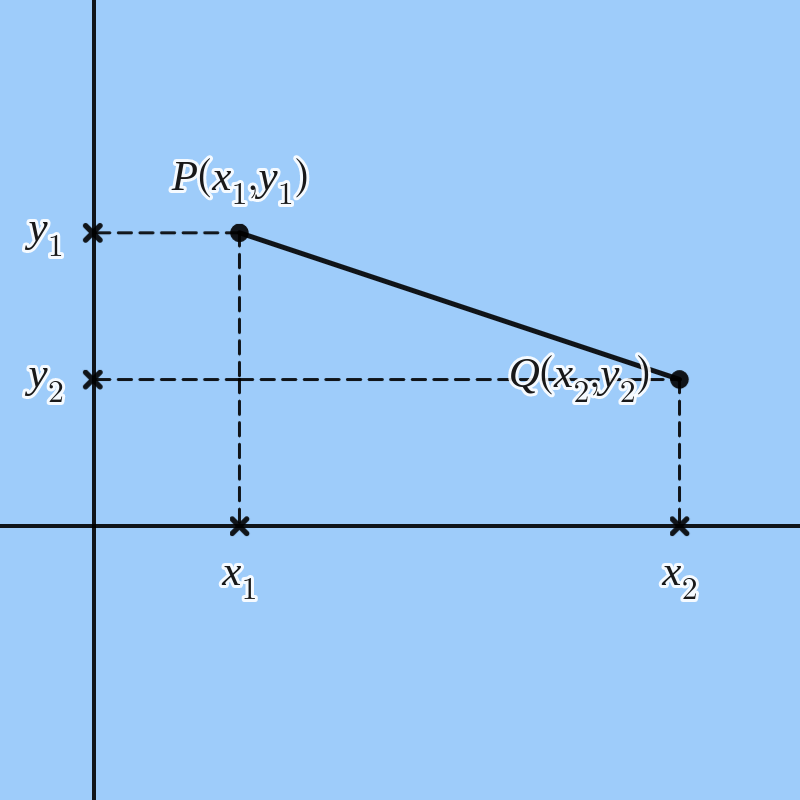
Gegeven de punten \(P(x_1,y_1)\) en \(Q(x_2,y_2)\text{.}\) De afstand \(d(P,Q)=|PQ|\) tussen deze twee punten in het vlak is gelijk aan de norm van \(\vv{PQ}\text{.}\)
\begin{align*}
|PQ|= \; \amp ||\vv{PQ}||=||\vv{Q}-\vv{P}|| \\
= \; \amp \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
\end{align*}
In principe kan je met bovenstaande formule elke afstand in het vlak berekenen door het probleem telkens te herleiden tot het het bepalen van de afstand tussen twee punten.
Voorbeeld 3.4.1. Afstand van een punt tot een rechte.
Stel dat we de afstand willen berekenen van het punt \(Q(6,3)\) tot de rechte \(a\) met cartesische vergelijking \(x+2y-6=0\text{.}\) Een normaalvector van deze rechte is \(\vv{N}(1,2)\) en de vergelijking van de loodlijn uit \(Q\) op \(a\) is bijgevolg \(2(x-6)-(y-3)=0\text{.}\) Het snijpunt van de loodlijn met \(a\) is het punt \(Q'\) met coordinaten
\begin{equation*}
\begin{cases}
x+2y-6 = 0 \\
2x-y-9=0
\end{cases} \Leftrightarrow
\begin{cases}
x=\frac{24}{5} \\
y=\frac{3}{5}
\end{cases}
\end{equation*}
De gezochte afstand is dus \(|QQ'|=\frac{6}{5}\sqrt{5}\text{.}\)
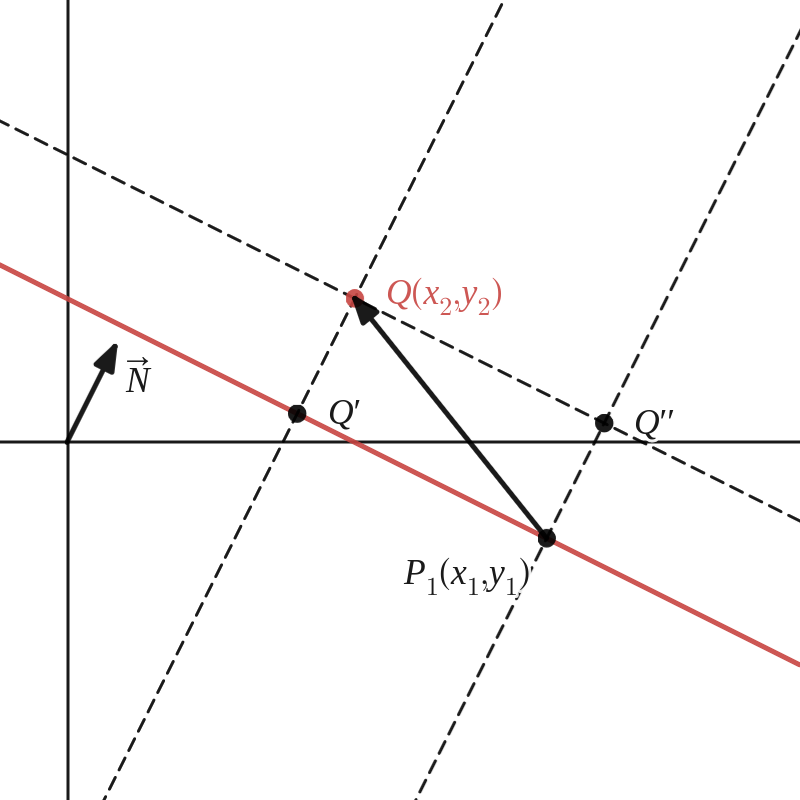
We kunnen het gestelde probleem ook algemeen aanpakken en een formule afleiden voor de afstand van een punt \(Q(x_2,y_2)\) tot de rechte \(a\) met vergelijking \(ux+vy+w=0\text{.}\) We nemen een willekeurig punt \(P_1(x_1,y_1)\) van de rechte en beschouwen de vector \(\overrightarrow{P_1Q}\text{.}\) De afstand \(d(Q,a)\) is dan gelijk aan de afstand \(d(P_1,Q'')\) waarbij \(\overrightarrow{P_1Q''}\) de component is van \(\overrightarrow{P_1Q}\) volgens de normaalvector \(\vv{N}(u,v)\) van de rechte.
Er geldt dat
\begin{align*}
\amp \overrightarrow{P_1Q}=\overrightarrow{P_1Q'}+\overrightarrow{P_1Q''}\\
\Rightarrow \amp \overrightarrow{P_1Q} \cdot \vv{N} = \overrightarrow{P_1Q'} \cdot \vv{N} + \overrightarrow{P_1Q''} \cdot \vv{N} \\
\Rightarrow \amp \overrightarrow{P_1Q} \cdot \vv{N} = \overrightarrow{P_1Q''} \cdot \vv{N}
\end{align*}
Aangezien de hoek tussen \(\overrightarrow{P_1Q''}\) en \(\vv{N}\) gelijk is aan \(0^{\circ}\) of \(180^{\circ}\) is het scalair product gelijk aan
\begin{equation*}
\overrightarrow{P_1Q''} \cdot \vv{N} = \pm ||\overrightarrow{P_1Q''}|| \cdot ||\vv{N}||
\end{equation*}
We krijgen dus uiteindelijk dat
\begin{align*}
d(Q,a)= \amp ||\overrightarrow{P_1Q''}|| =\frac{|\overrightarrow{P_1Q''} \cdot \vv{N} |}{||\vv{N}||}\\
\amp =\frac{|\overrightarrow{P_1Q} \cdot \vv{N} |}{||\vv{N}||} \\
= \amp \frac{|(x_2-x_1,y_2-y_1) \cdot (u,v)|}{\sqrt{u^2+v^2}}\\
= \amp \frac{|u(x_2-x_1)+v(y_2-y_1)|}{\sqrt{u^2+v^2}}
\end{align*}
Aangezien \(P_1\) een punt is van de rechte \(a\) geldt er dat \(ux_1+vy_1+w=0\text{.}\) We kunnen de teller van bovenstaande formule dus herschrijven tot
\begin{equation*}
u(x_2-x_1)+v(y_2-y_1)=ux_2+vy_2-ux_1-vy_1=ux_2+vy_2+w
\end{equation*}
Afstand van een punt tot een rechte.
De afstand van het punt \(Q(x_2,y_2)\) tot de rechte \(a\) met cartesische vergelijking \(ux+vy+w=0\) is
\begin{equation*}
d(Q,a)= \frac{|ux_2+vy_2+w|}{\sqrt{u^2+v^2}}
\end{equation*}
Je kan dezelfde formule natuurlijk ook gebruiken om de afstand tussen twee evenwijdige rechten te berekenen.