Hoek tussen twee rechten

Sectie 3.2 Hoek tussen twee rechten

Voorbeeld 3.2.1. De hoek tussen twee rechten bepalen m.b.v. het scalair product.

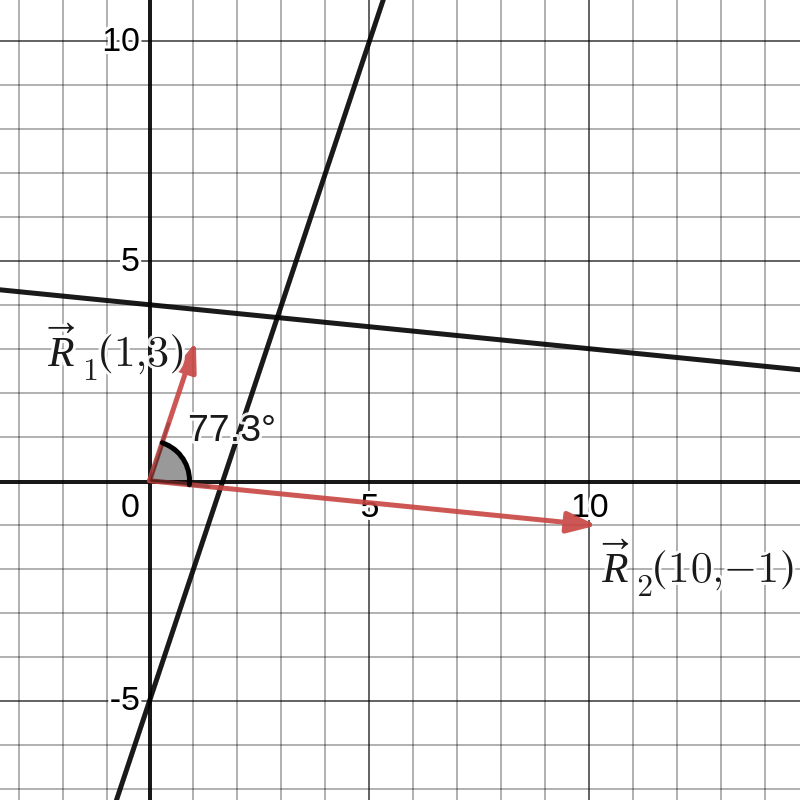
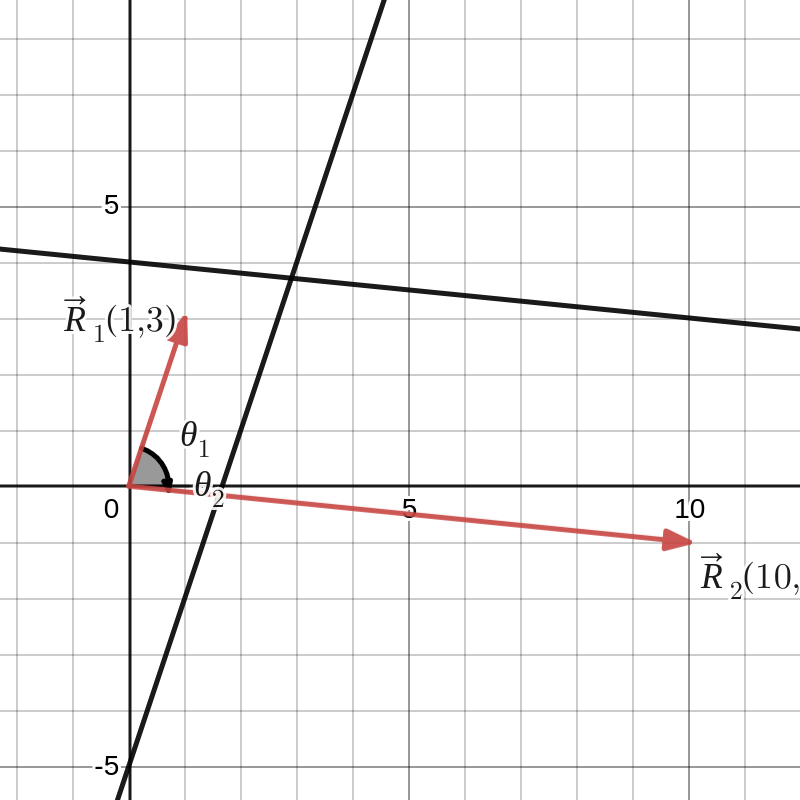
We bepalen de hoek tussen de rechten \(y=3x-5\) en \(y=-\dfrac{x}{10}+4\text{.}\) Twee richtingsvectoren zijn \(\vv{R}_1(1,3)\) en \(\vv{R}_2 (10,-1)\text{.}\) De hoek tussen de twee rechten is gelijk aan de hoek tussen de twee richtingsvectoren. De cosinus van de gezochte hoek is

\begin{equation*} \cos \theta =\frac{\vv{R}_1 \cdot \vv{R}_2}{||\vv{R}_1|| \cdot ||\vv{R}_2||}=\dfrac{7}{\sqrt{10} \sqrt{101}} \end{equation*}

en de hoek zelf is \(\theta = 77,3^{\circ}\)

Hoek tussen twee rechten.

De hoek tussen twee rechten kan je bepalen door de hoek tussen hun richtingsvectoren te bepalen. Let wel op de zin van de richtingsvectoren zodat je de scherpe hoek bepaalt!

Voorbeeld 3.2.2. De hoek tussen twee rechten bepalen m.b.v. de verschilformule voor tangens.

De hoek tussen twee rechten kan ook bepaald worden met de verschilformule voor tangens. We illustreren dit door bovenstaand voorbeeld te hernemen. Stel dat \(\theta_1\) de hoek is tussen \(\vv{R}_1\) en de \(x\)-as en \(\theta_2\) de hoek tussen \(\vv{R}_2\) en de \(x\)-as

In dit voorbeeld is \(\theta_2\) negatief!

. De hoek \(\theta\) tussen \(\vv{R}_1\) en \(\vv{R}_2\) kan dan ook bepaald worden via

\begin{align*} \tan \theta = \; \amp \tan(\theta_1 - \theta_2)\\ = \; \amp \frac{\tan \theta_1 - \tan \theta_2}{1+\tan \theta_1 \tan \theta_2}\\ = \; \amp \frac{m_1 - m_2}{1+m_1 m_2} \end{align*}

met \(m_1\) en \(m_2\) de richtingscoëfficiënten van de twee rechten. Invullen van \(m_1=3\) en \(m_2=-\dfrac{1}{10}\) geeft \(\theta = \tan^{-1}\left (\dfrac{31}{7} \right) = 77,3\g\text{.}\)

Loodrechte stand van twee rechten.

Gegeven een rechte \(e\) met richtingsvector \(\vv{R_1}(a_1,b_1)\) en een rechte \(f\) met richtingsvector \(\vv{R_2}(a_2,b_2)\text{.}\) De rechten \(e\) en \(f\) staan loodrecht op elkaar als en slechts als hun richtingsvectoren loodrecht op elkaar staan:

\begin{equation*} e \perp f \Leftrightarrow \vv{R_1} \cdot \vv{R_2} = 0 \Leftrightarrow a_1a_2+b_1b_2=0 \end{equation*}

Voorbeeld 3.2.3.

Twee richtingsvectoren van de rechten \(y=3x-5\) en \(y=-\dfrac{1}{3}+2\) zijn \(\vv{R}_1(1,3)\) en \(\vv{R}_2 (-3,1)\) en er geldt dat

\begin{equation*} \vv{R}_1 \cdot \vv{R}_2 = (1,3) \cdot (-3,1)= 0 \end{equation*}

Deze rechten staan bijgevolg loodrecht op elkaar.

Veralgemenen we de redenering uit bovenstaand voorbeeld, dan volgt hieruit onmiddellijk de eigenschap dat twee rechten loodrecht op elkaar staan als en slechts als het product van hun richtingscoëfficienten gelijk is aan \(-1\text{:}\)

Gegeven twee rechten \(y=m_1x+q_1\) en \(y=m_2x+q_2\text{.}\)
Twee richtingsvectoren zijn \(\vv{R}_1(1,m_1)\) en \(\vv{R}_2 (1,m_2)\text{.}\)
De twee rechten staan loodrecht op elkaar als en slechts als

\begin{align*} \amp \vv{R}_1 \cdot \vv{R}_2 = 0\\ \Leftrightarrow \; \amp (1,m_1) \cdot (1,m_2) = 0 \\ \Leftrightarrow \; \amp 1+m_1m_2 = 0 \\ \Leftrightarrow \; \amp m_1m_2 = -1 \end{align*}

Opdracht 3.2.1.

Gegeven de rechte \(e\) met parametervoorstelling

\begin{equation*} \begin{cases} x = -3+4k \\ y= -3-3k \end{cases} \quad (k \in \mathbb{R}) \end{equation*}

Bepaal een parametervoorstelling en een cartesische vergelijking van de rechte \(f\) door het punt \((1,2)\) en loodrecht op de rechte \(e\text{.}\)

Oplossing.

Een richtingsvector van de gegeven rechte is \(\vv{R}_e(4,-3)\) en een richtingsvector \(\vv{R}_f(a,b)\) van de rechte \(f\) moet voldoen aan

\begin{equation*} 4a-3b=0 \Rightarrow \vv{R}_f(3,4) \end{equation*}

Een mogelijke parametervoorstelling is dus

\begin{equation*} f \leftrightarrow \begin{cases} x = 1+3k \\ y= 2+4k \end{cases} \quad (k \in \mathbb{R}) \end{equation*}

en een cartesische vergelijking

\begin{equation*} \dfrac{x-1}{3}=\dfrac{y-2}{4} \Leftrightarrow 4x-3y+2=0 \end{equation*}

Vorig Top Volgend