Vectoren en puntvectoren.
Een vector is gelijk aan het verschil van de puntvectoren van zijn eindpunt en zijn beginpunt:
\begin{align*}
\vv{PQ} \amp =\vv{PO}+\vv{OQ} \\
\amp = -\vv{OP}+\vv{OQ} \\
\amp = \vv{Q}-\vv{P}
\end{align*}
Sectie 1.6 Puntvectoren
We kiezen in het vlak een willekeurig punt \(O\) als oorsprong. Elk punt \(P\) bepaalt nu een vector \(\vv{OP}\text{.}\) Aangezien \(O\) een vast punt is noteren we dit kort als:
\begin{equation*}
\vv{P}=\vv{OP}
\end{equation*}
\(\vv{P}\) noemen we de puntvector of plaatsvector van het punt \(P\text{.}\) Aangezien er met elk punt van het vlak een puntvector correspondeert, gebruiken we de termen punt en puntvector vanaf nu door elkaar.
Opdracht 1.6.1. Midden van een lijnstuk.
Bepaal de puntvector van het midden van het lijnstuk \([AB]\text{.}\)
Het midden van een lijnstuk.
\(\vv{M}\) is het midden van het lijnstuk \([AB] \Leftrightarrow \vv{M}=\dfrac{\vv{A}+\vv{B}}{2}\)
We vermelden, voorlopig zonder bewijs, de formule voor de puntvector van het zwaartepunt van een driehoek.
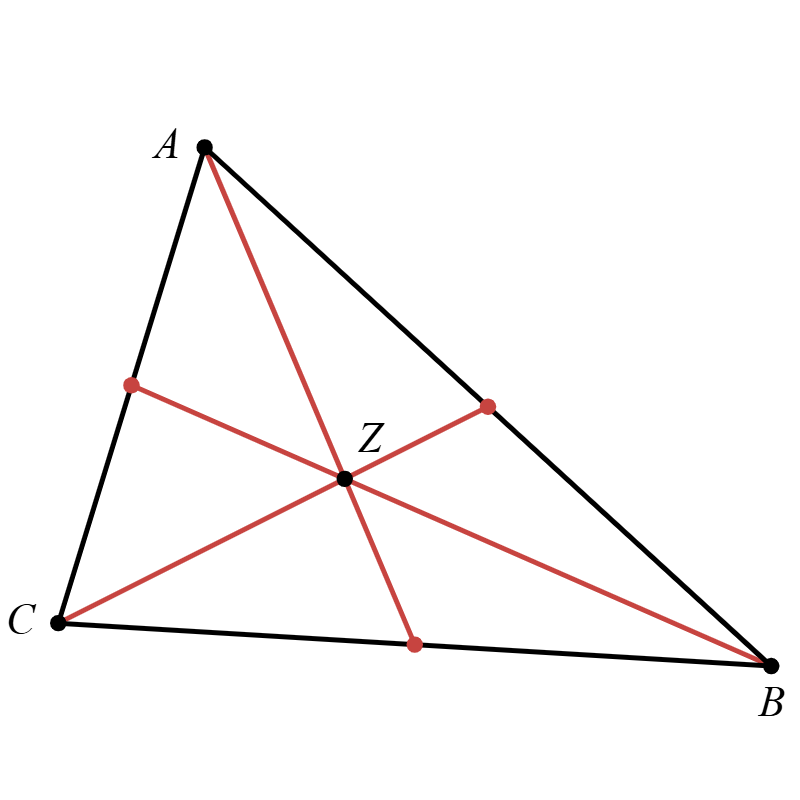
Zwaartepunt van een driehoek.
Een zwaartelijn van een driehoek is een rechte die door een hoekpunt en het midden van de overstaande zijde gaat. De zwaartelijnen snijden elkaar in het zwaartepunt.
\(\vv{Z}\) is het zwaartepunt van de driehoek \(ABC\) \(\Leftrightarrow \vv{Z}=\dfrac{\vv{A}+\vv{B}+\vv{C}}{3}\)
