Sectie 3.3 De normaalvector en de cartesische vergelijking van een rechte
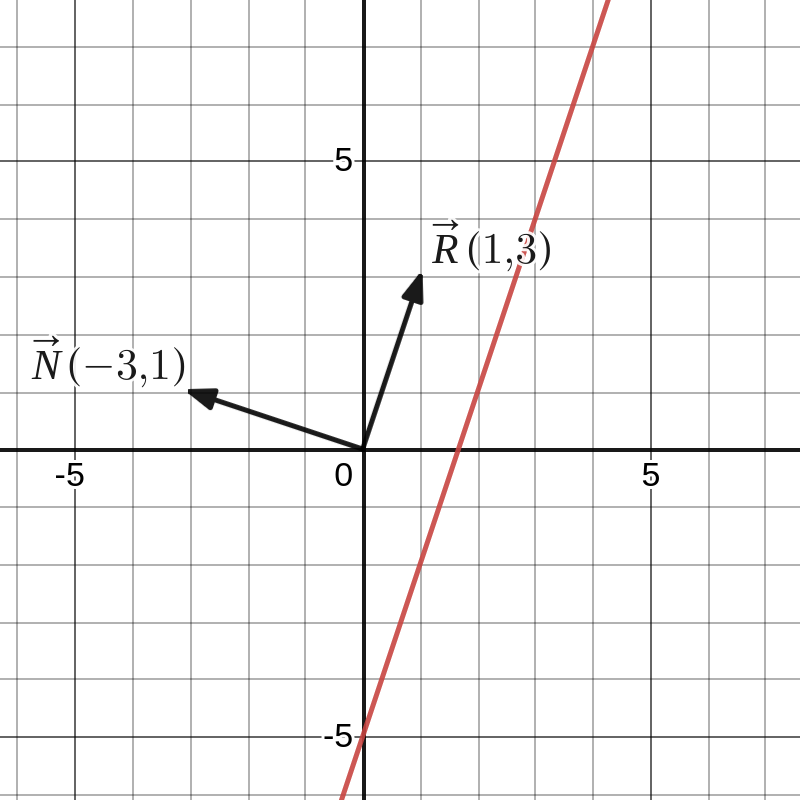
Een normaalvector \(\vv{N}\) is een vector die loodrecht staat op de richting van een rechte (en dus loodrecht op een willekeurige richtingsvector). Voor de rechte \(y=3x-5\) is \(\vv{R}(1,3)\) een richtingsvector en \(\vv{N}(-3,1)\) een normaalvector. Een rechte heeft eveneens een oneindig aantal normaalvectoren die allemaal een veelvoud van elkaar zijn.
Met behulp van de normaalvector en het scalair product kan de algemene cartesische vergelijking van een rechte in een orthonormaal assenstelsel afgeleid worden.
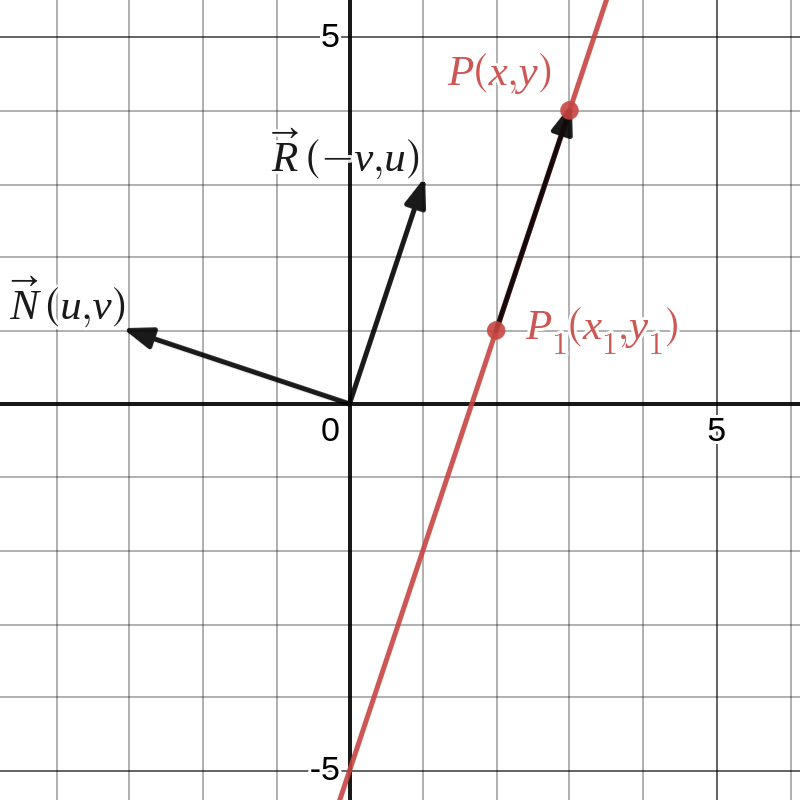
\(\vv{N}(u,v)\) is een normaalvector van de rechte door een punt \(\vv{P}_1(x_1,y_1)\) als en slechts als
\begin{align*}
\amp \vv{N} \cdot \vv{P_1P}=0\\
\amp \vv{N} \cdot (\vv{P}-\vv{P_1})=0\\
\Leftrightarrow \; \amp (u,v) \cdot (x-x_1,y-y_1) =0 \\
\Leftrightarrow
\; \amp u(x-x_1)+v(y-y_1) = 0
\end{align*}
De algemene vorm van de cartesische vergelijking van een rechte door een gegeven punt \(P_1(x_1,y_1)\) en met een gegeven normaalvector \(\vv{N}(u,v)\) is dus
\begin{equation*}
\boxed{u(x-x_1)+v(y-y_1) = 0}
\end{equation*}
Uitwerken levert
\begin{equation*}
ux+vy-ux_1-vy_1=0
\end{equation*}
Stellen we de constante term \(-ux_1-vy_1\) gelijk aan \(w\text{,}\) dan wordt de vergelijking \(ux+vy+w=0\text{.}\)
Normaalvector en cartesische vergelijking van een rechte.
Voor de rechte met cartesische vergelijking \(ux+vy+w=0\) is
\(\vv{N}(u,v)\) een normaalvector
\(\vv{R}(-v,u)\) een richtingsvector
Als \(P_1(x_1,y_1)\) een punt van de rechte is, kan de vergelijking ook geschreven worden als
\begin{equation*}
u(x-x_1)+v(y-y_1)=0
\end{equation*}
Voorbeeld 3.3.1. Cartesische vergelijking bepalen m.b.v. de normaalvector.
Gegeven de rechte met parametervoorstelling
\begin{equation*}
\begin{cases}
x=-1+3k \\ y = 4 -5 k
\end{cases} \qquad (k \in \mathbb{R})
\end{equation*}
Een richtingsvector is \(\vv{R}(3,-5)\) en een normaalvector \(\vv{N}(5,3)\text{.}\) De cartesische vergelijking van de rechte is bijgevolg
\begin{equation*}
5(x+1)+3(y-4) = 0 \Leftrightarrow 5x + 3y - 7 =0
\end{equation*}