Naar de hoofdinhoud

Goniometrie en complexe getallen: 3de graad ASO met 5 of 7 lesuren per week

Nele Vermeulen

Sectie 1.4 Goniometrische getallen van willekeurige hoeken

Subsectie 1.4.1 De goniometrische cirkel

De goniometrische cirkel is een onmisbaar hulpmiddel en vormt de basis van de uitbreiding van de goniometrische getallen voor hoeken groter dan \(90^{\circ}\text{.}\)

Goniometrische cirkel.

De goniometrische cirkel is de cirkel met de oorsprong als middelpunt en met een straal gelijk aan 1. De cartesische vergelijking is
\begin{equation*} x^2+y^2=1 \end{equation*}
De goniometrische cirkel wordt onderverdeeld in vier vier kwadranten.
We gaan nu georiënteerde hoeken beschouwen met als eerste been de positieve \(x\)-as en als tweede been de halfrechte \([OP\text{,}\) met \(P\) een willekeurig punt van de goniometrische cirkel. Het punt \(P\) noemen we het beeldpunt van die hoek.
Een punt op de goniometrische cirkel is het beeldpunt van oneindig veel hoeken. Zo is het beeldpunt van \(-30^{\circ}\) ook het beeldpunt van
\begin{align*} \amp -30^{\circ}+360^{\circ}=330^{\circ}\\ \amp -30^{\circ}+2 \cdot 360^{\circ}=690^{\circ}\\ \amp -30^{\circ}-360^{\circ}=-390^{\circ} \end{align*}
Als \(P\) het beeldpunt is van een hoek \(\alpha\text{,}\) dan is \(P\) eveneens het beeldpunt van de hoeken \(\alpha+k\cdot 360^{\circ}\) of \(\alpha + k\cdot 2\pi\) met \(k \in \mathbb{Z}\text{.}\)

Subsectie 1.4.2 Sinus, cosinus en tangens

In het eerste kwadrant volgt uit de definitie van sinus en cosinus in een rechthoekige driehoek dat de coördinaat van een punt op de goniometrische cirkel gelijk is aan \((\cos \alpha, \sin \alpha)\) (zie onderstaande tekening). In de andere kwadranten gebruiken we dit om cosinus en sinus te definiëren.

Sinus en cosinus.

\(\cos \alpha\) is de \(x\)-coördinaat en \(\sin \alpha\) is de \(y\)-coördinaat van het beeldpunt van de hoek \(\alpha\text{.}\) Hieruit volgt natuurlijk onmiddellijk dat
\begin{align*} \amp -1 \le \sin \alpha \le 1\\ \amp -1 \le \cos \alpha \le 1 \end{align*}
De cosinus- en sinuswaarden voor alle bijzondere hoeken heb je bijgevolg al bepaald in Oefening 1.5.51

Tangens.

De tangens van een willekeurige hoek \(\alpha\) definiëren we als
\begin{equation*} \tan \alpha = \frac{\sin \alpha}{\cos \alpha} \quad (\text{met} \cos \alpha \neq 0) \end{equation*}
Alternatief kan \(\tan \alpha\) ook gedefinieerd worden als de \(y\)-coördinaat van het snijpunt van de rechte \(OP\) met de raaklijn aan de goniometrische cirkel in het punt \((1,0)\text{.}\)
Merk op dat \(\tan \alpha\) eveneens de richtingscoëfficiënt is van de rechte \(OP\text{:}\)
\begin{equation*} \textrm{rechte } OP \leftrightarrow y = \tan \alpha \cdot x \end{equation*}
Er geldt steeds dat
\begin{equation*} -\infty \le \tan \alpha \le +\infty \end{equation*}

Opdracht 1.4.1.

Gegeven de rechte \(y=\dfrac{2}{5}x\text{.}\)
  1. Teken deze rechte.
  2. Bereken de hoek die deze rechte maakt met de positieve \(x\)-as zowel in graden als in radialen. Vanaf nu zullen we deze hoek de hellingshoek \(\theta\) noemen.
  3. Voeg de goniometrische cirkel toe aan de tekening en duid de beeldpunten aan van de hoeken waarvan de tangens gelijk is aan \(\tan \theta\text{.}\)
  4. Bereken alle hoeken \(\in ]\pi,\pi]\) die je net aangeduid hebt.
  5. Bereken tenslotte de coördinaten van de aangeduide beeldpunten.

Opdracht 1.4.2.

In bovenstaande tekening zie je drie gelijkvormige driehoeken. Vervolledig de figuur met de lengtes van de zijden en gebruik de gelijkvormigheid om aan te tonen dat
\begin{align*} \amp \frac{\sin \theta}{\cos \theta} = \frac{\tan \theta}{1} = \frac{1}{\cot \theta} \end{align*}
Hierboven staat eigenlijk gewoon de definitie van de tangens en de cotangens. De gelijkvormigheid leidt ook tot
\begin{align*} \amp \frac{\sin \theta}{1} = \frac{\tan \theta}{y} =\frac{1}{x} \end{align*}
Schrijf uitdrukkingen op voor \(x\) en \(y\) en vereenvoudig zoveel mogelijk.

Subsectie 1.4.3 Cotangens, secans en cosecans

De sinus, cosinus en tangens zijn de belangrijkste goniometrische getallen. De andere zijn:
  • De cotangens, gedefinieerd als \(\cot \alpha=\dfrac{1}{\tan \alpha}=\dfrac{\cos \alpha}{\sin \alpha}\) als \(\sin \alpha \neq 0\text{.}\) Meetkundig gezien is \(\cot \alpha\) de \(x\)-coördinaat van het snijpunt van de rechte \(OP\) met de raaklijn aan de cirkel in het punt \((0,1)\text{.}\)
  • De secans, gedefinieerd als \(\sec \alpha=\dfrac{1}{\cos \alpha}\) als \(\cos \alpha \neq 0\text{.}\) Meetkundig gezien is de secans de \(x\)-coördinaat van het snijpunt van de raaklijn aan de cirkel in het beeldpunt \(P\) met de \(x\)-as.
  • De cosecans, gedefinieerd als \(\csc \alpha=\dfrac{1}{\sin \alpha}\) als \(\sin \alpha \neq 0\text{.}\) Meetkundig gezien is de cosecans de \(y\)-coördinaat van het snijpunt van de raaklijn aan de cirkel in het beeldpunt \(P\) met de \(y\)-as.
Deze goniometrische getallen zijn voornamelijk handig om breuken in goniometrische uitdrukkingen te vermijden.
Op onderstaande interactieve tekening kan je de sinus, cosinus, tangens en cotangens visualiseren voor een willekeurige hoek \(\alpha.\)

Opdracht 1.4.3.

  1. Verklaar de meetkundige betekenis van de secans en de cosecans, d.w.z. toon aan dat \(|OQ|=\sec \alpha\) en \(|OR|=\csc \alpha\text{.}\)
  2. Leg uit waarom \(|PQ|=\tan \alpha\text{.}\)
  3. Druk de lengte \(|OP|\) uit in termen van de goniometrische getallen van de hoek \(\alpha\) (zie onderstaande tekening).
Oplossing.
  1. Bereken cosinus in rechthoekige driehoek \(OPQ\) en sinus in rechthoekige driehoek \(OPR\text{.}\)
  2. Bereken tangens in rechthoekige driehoek \(OPQ\text{.}\)
  3. \(1+\tan^2 \alpha=\dfrac{1}{\cos^2 \alpha}= \sec^2 \alpha\text{.}\)

Subsectie 1.4.4 Verwante hoeken

  • \(\alpha\) en \(\beta\) zijn tegengestelde hoeken \(\Leftrightarrow \beta = -\alpha + 2k \pi\) (\(k \in \mathbb{Z}\)).
    \begin{align*} \amp \cos(-\alpha)=\cos \alpha \\ \amp \sin(-\alpha)=-\sin \alpha\\ \amp \tan(-\alpha)=-\tan \alpha \\ \amp \cot(-\alpha)=-\cot \alpha \end{align*}
  • \(\alpha\) en \(\beta\) zijn supplementaire hoeken \(\Leftrightarrow \beta = \pi -\alpha + 2k \pi\) (\(k \in \mathbb{Z}\)).
    \begin{align*} \amp \cos(\pi-\alpha)=-\cos \alpha\\ \amp \sin(\pi-\alpha)=\sin \alpha \\ \amp \tan(\pi-\alpha)=-\tan \alpha \\ \amp \cot(\pi-\alpha)=-\cot \alpha \end{align*}
  • \(\alpha\) en \(\beta\) zijn antisupplementaire hoeken \(\Leftrightarrow \beta = \pi + \alpha + 2k \pi\) (\(k \in \mathbb{Z}\)).
    \begin{align*} \amp \cos(\pi+\alpha)=-\cos \alpha\\ \amp \sin(\pi+\alpha)=-\sin \alpha \\ \amp \tan(\pi+\alpha)=\tan \alpha \\ \amp \cot(\pi+\alpha)=\cot \alpha \end{align*}
  • \(\alpha\) en \(\beta\) zijn complementaire hoeken \(\Leftrightarrow \beta = \dfrac{\pi}{2} - \alpha + 2k \pi\) (\(k \in \mathbb{Z}\)).
    \begin{align*} \amp \sin \left (\dfrac{\pi}{2}-\alpha \right ) =\cos \alpha\\ \amp \cos \left (\dfrac{\pi}{2}-\alpha \right ) =\sin \alpha \\ \amp \tan \left (\dfrac{\pi}{2}-\alpha \right )=\cot \alpha \\ \amp \cot \left (\dfrac{\pi}{2}-\alpha \right )=\tan \alpha \end{align*}

Opmerking 1.4.1.

Memoriseer de verbanden tussen de goniometrische getallen niet, maar oefen op het aflezen ervan m.b.v. de goniometrische cirkel. Je moet ook in staat zijn om het verband op te schrijven tussen bijvoorbeeld \(\cos \left (\frac{3\pi}{2} + \alpha \right )\) en een goniometrisch getal van de hoek \(\alpha\text{.}\)

Opdracht 1.4.4.

Overtuig jezelf m.b.v. de goniometrische cirkel dat
\begin{align*} \amp \cos \left (\frac{3\pi}{2} + \alpha \right ) = \sin \alpha\\ \amp \sin \left (\frac{3\pi}{2} + \alpha \right ) = -\cos \alpha \end{align*}

Voorbeeld 1.4.2. Herleiden naar het eerste kwadrant.

Met behulp van de formules voor verwante hoeken kan je goniometrische getallen van hoeken in het tweede, derde of vierde kwadrant berekenen door deze te herleiden naar de goniometrische getallen van hoeken in het eerste kwadrant. Enkele voorbeelden:
\begin{align*} \amp \cos 165^{\circ} = \cos \left (180^{\circ} - 15^{\circ} \right) = - \cos 15^{\circ}\\ \amp \sin \left ( \frac{13 \pi}{4} \right ) = \sin \left ( \frac{13 \pi}{4} -2\pi \right )= \sin \left ( \frac{5 \pi}{4} \right ) = \sin \left ( \pi + \frac{\pi}{4} \right ) = - \sin \frac{\pi}{4}\\ \amp \cot \left (-65^{\circ} \right ) = - \cot 65^{\circ} \end{align*}

Subsectie 1.4.5 Formules van de goniometrie voor willekeurige hoeken

De geziene goniometrische formules (zie Formules van de goniometrie) blijven gelden voor hoeken in de andere kwadranten. We nemen dit aan zonder bewijs, maar bewijzen wel enkele formules opnieuw door te steunen op verwante hoeken.

Voorbeeld 1.4.3. \(\cos (\alpha - \beta)\) via tegengestelde hoeken.

De formule voor \(\cos (\alpha - \beta)\) kan opgesteld worden op basis van de formule voor \(\cos(\alpha + \beta)\text{:}\)
\begin{align*} \cos ( \alpha - \beta) = \; \amp \cos (\alpha + (-\beta)) \\ = \; \amp \cos \alpha \cos(-\beta) - \sin \alpha \sin(-\beta) \qquad (\text{formule }\cos (\alpha + \beta)\\ = \; \amp \cos \alpha \cos \beta + \sin \alpha \sin \beta \qquad (\text{formules tegengestelde hoeken)}\ \end{align*}

Opdracht 1.4.5.

(a)
Stel de formule voor \(\tan(\alpha - \beta)\) op door te steunen op de formule voor \(\tan(\alpha + \beta)\) en de formules voor tegengestelde hoeken.
(b)
Stel de formule voor \(\cos(\alpha + \beta)\) op door te steunen op de formule voor \(\sin(\alpha - \beta)\) en de formules voor complementaire hoeken.

Subsectie 1.4.6 De sinus- en de cosinusregel

Een willekeurige driehoek kan altijd opgelost worden door die te verdelen in twee rechthoekige driehoeken, maar met de sinus- en de cosinusregel kunnen we dit eenvoudiger en sneller aanpakken.

De sinusregel en de cosinusregel.

De sinusregel stelt dat in een willekeurige driehoek de verhouding van de lengte van een zijde tot de sinus van de overstaande hoek constant is:
\begin{equation*} \frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma} \end{equation*}
De cosinusregel is de uitbreiding van de stelling van Pythagoras voor willekeurige driehoeken:
\begin{align*} \amp a^2=b^2+c^2-2bc \cos \alpha \\ \amp b^2=a^2+c^2-2ac \cos \beta \\ \amp c^2 = a^2 + b^2 - 2ab \cos \gamma \end{align*}

Voorbeeld 1.4.4. Toepassing van de sinus- en cosinusregel.

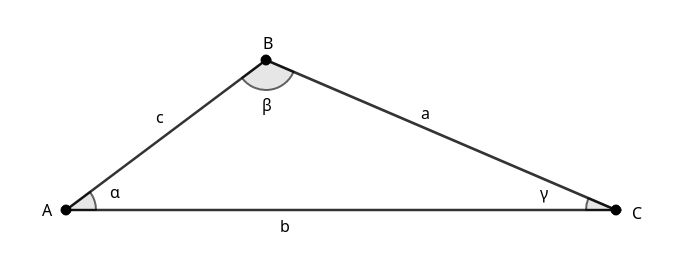
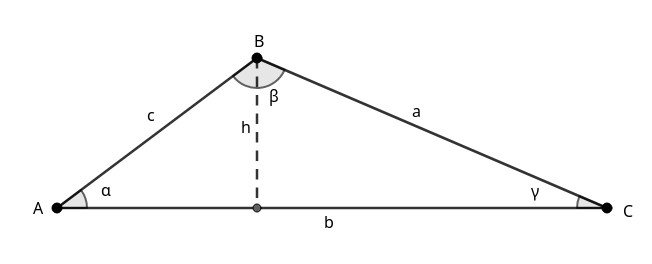
Gegeven een driehoek met zijden \(a = 7\) cm, \(b = 9\) cm, en hoek \(\gamma = 60^\circ\text{.}\) Bereken zijde \(c\) en de overige hoeken tot op twee decimalen nauwkeurig.
We gebruiken eerst de cosinusregel om \(c\) te berekenen:
\begin{equation*} c^2 = 7^2 + 9^2 - 2 \cdot 7 \cdot 9 \cdot \cos 60^\circ \end{equation*}
\begin{equation*} c^2 = 49 + 81 - 63 = 67 \quad \Rightarrow \quad c = \sqrt{67} \end{equation*}
En vervolgens de sinusregel om hoek \(\alpha\) te berekenen:
\begin{equation*} \frac{\sin \alpha}{7} = \frac{\sin 60^\circ}{\sqrt{67}} \end{equation*}
\begin{equation*} \sin \alpha = \frac{7 \cdot \sin 60^\circ}{\sqrt{67}} \end{equation*}
Hieruit volgt dan \(\alpha = 47,78^{\circ} \) en \(\beta = 180^\circ - \alpha - 60^\circ=72,22^\circ\text{.}\)

Opdracht 1.4.6.

(a)
Toon aan dat in een rechthoekige driehoek de sinusregel zich herleidt tot de definitie van de sinus van een scherpe hoek.
(b)
Toon aan dat in een rechthoekige driehoek de cosinusregel zich herleidt tot de stelling van Pythagoras.

Opdracht 1.4.7. Bewijs van de sinusregel.

(a)
Toon aan \(a \sin \gamma = c \sin \alpha\) door de hoogte \(h\) op twee verschillende manieren te berekenen. Hieruit volgt al onmiddelijk het eerste deel van de sinusregel.
(b)
Voeg een hoogte \(h'\) toe aan bovenstaande tekening en bewijs het tweede deel van de sinusregel.

Opdracht 1.4.8. Bewijs van de cosinusregel.

Bewijs dat \(a^2=b^2+c^2-2bc \cos \alpha\) (de andere twee verlopen analoog). Gebruik opnieuw onderstaande tekening.
VorigTopVolgend