A mathematician, like a painter or a poet, is a maker of patterns. If his patterns are more permanent than theirs, it is because they are made with ideas.―G. H. Hardy (1877-1947) in A Mathematician’s Apology.
Hoofdstuk 1 Wiskunde is de wetenschap van patronen
Over de vraag “Wat is wiskunde?” zijn er hele boeken geschreven. Het is een boeiend vak met veel facetten en één van de belangrijkste menselijke verwezenlijkingen. Wiskunde wordt weleens de wetenschap van patronen genoemd en het is deze invalshoek waar eerst even kort bij stilstaan.
Patronen spelen sowieso een belangrijke rol in de wiskunde. Enkele eenvoudige voorbeelden:
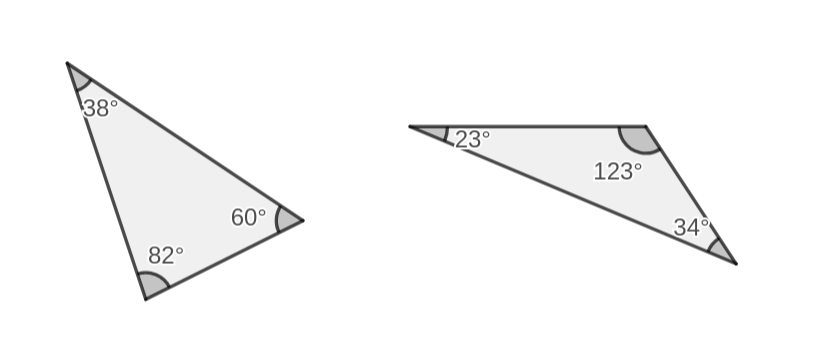
- In een driehoek
-
is de som van de hoeken altijd gelijk aan \(180\g\)
-
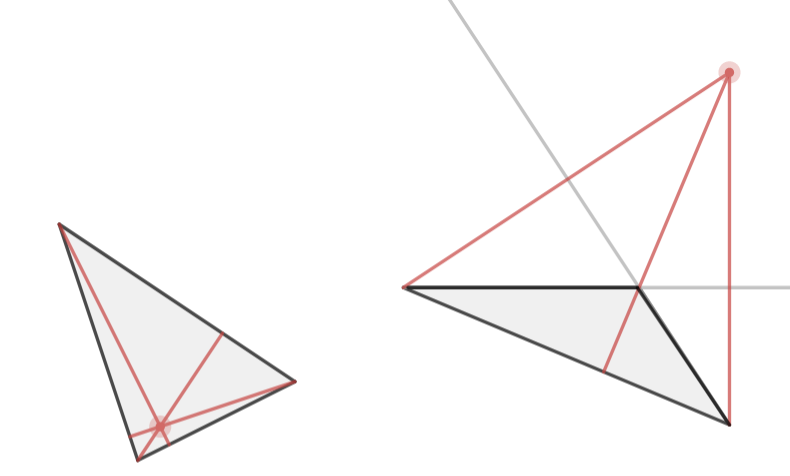
gaan de hoogtelijnen altijd door één punt.
-
- Elk natuurlijk getal kan op een unieke manier geschreven worden als een product van priemgetallen:\begin{align*} \amp 20 = 2^2 \cdot 5 \amp 25 \amp = 5^2\\ \amp 21 = 3 \cdot 7 \amp 26 \amp = 2 \cdot 13 \\ \amp 22 = 2 \cdot 11 \amp 27 \amp = 3^3\\ \amp 23 \amp 28 \amp = 2^2 \cdot 7 \\ \amp 24 = 2^3 \cdot 3 \amp 29 \amp \end{align*}
- Het irrationaal getal \(\pi\) kan geschreven worden als een oneindige som\begin{equation*} \frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\ldots \end{equation*}
Enkel het laatste voorbeeld kwam nog niet eerder aan bod in de wiskundelessen en dat zal jammer genoeg ook nog wel even duren.
Onderzoek 1.0.1.
(a) Even getallen (groter dan 2).
Bestudeer onderstaand rijtje van even getallen:
\begin{align*}
\amp 4 = 2 + 2 \\
\amp 6 = 3 + 3 \\
\amp 8 = 3 + 5 \\
\amp 14 = 3 + 11 = 7 + 7\\
\amp 18 = 5 + 13 = 7 + 11 \\
\amp 26 = 3 + 23 = 7 + 19\\
\amp 28 = 5 + 23 = 11 + 17 \\
\amp 36 = 5 + 31 = 7 + 29 = 13 +23 = 17 +19\\
\amp 60 = 7 + 53 = 13 + 47 = 17 + 43 = 9 + 41 = 23 + 37 = 29 + 31
\end{align*}
Welk patroon herken je? Formuleer dit zo beknopt mogelijk.
(b) Veelvouden van 3.
- Schrijf alle veelvouden van 3 op, groter dan 10 en kleiner dan 50.
- Tel de cijfers van elk getal op.
- Welk patroon merk je op? Formuleer dit zo beknopt mogelijk.
(c)
Gegeven het onderstaande patroon van drie tekeningen:
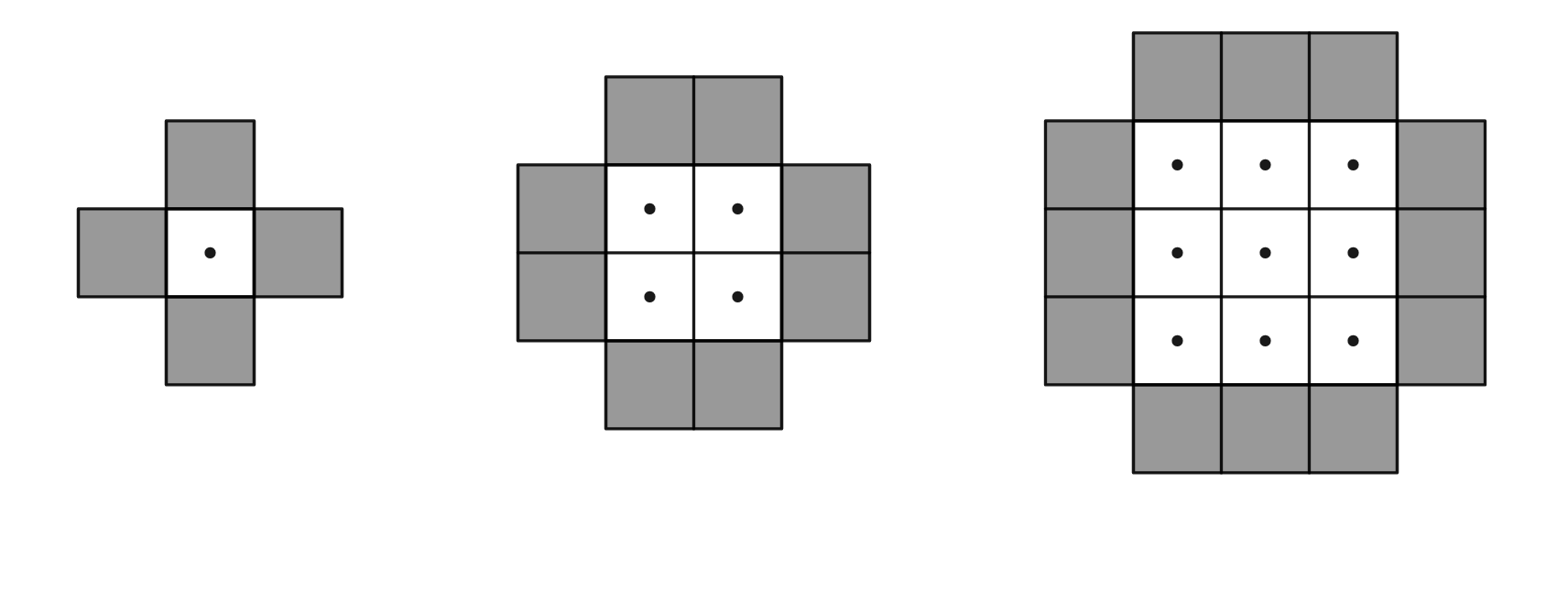
- Maak zelf de vierde tekening.
- Hoeveel bolletjes bevat tekening 8 van het patroon?
- Schrijf een uitdrukking op die het aantal gekleurde vierkantjes voor de \(n\)-de tekening van het patroon geeft.
(d)
Zoek zoveel mogelijk patronen in onderstaande driehoek van getallen.


